Quick algebra 1 question for 50 points!
Only answer if you know the answer, quick shout-out to Yeony2022, tysm for the help!
Answers
See
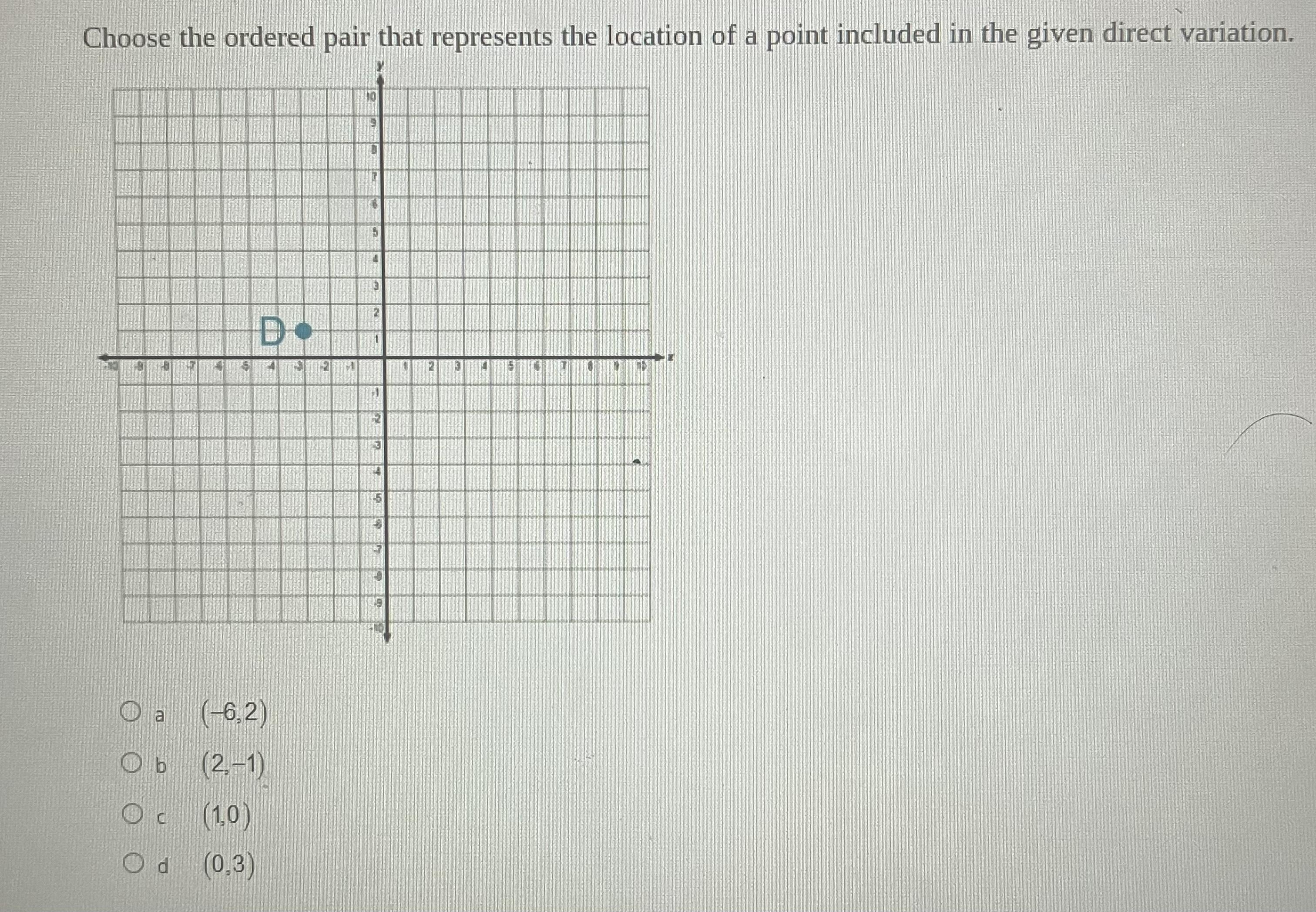
The point D is
3 units left from origin
x coordinate=-31 units up from origin
y coordinate=1The point is
(-3,1)Direct variation
Multiply k=2
k(-3,1)2(-3,1)(-6,2)Option A
Related Questions
How many different ways are there to choose 13 donuts if the shop offers 19 different varieties to choose from? Simplify your answer to an integer.
Answers
there are 27,132 different ways to choose 13 donuts out of 19 varieties.
This problem involves selecting 13 donuts out of 19 different varieties, without regard to order. This is a combination problem, and the number of combinations of n objects taken r at a time is given by the formula:
n! / (r!(n-r)!)
Using this formula, we can find the number of ways to choose 13 donuts out of 19:
19! / (13!(19-13)!) = 19! / (13!6!) = 27,132
what is combination?
Combination refers to the mathematical concept of choosing a subset of objects from a larger set, where the order of selection is not considered. In other words, combination is a way of selecting items from a group without any regard to the order in which the items are arranged.
To learn more about combination visit:
brainly.com/question/19692242
#SPJ11
Please help please please
Answers
The length of the side CD is 15.
We have,
In ΔABC,
Applying the Pythagorean theorem,
AC² = AB² + BC²
BC² = 10² - 6²
BC² = 100 - 36
BC² = 64
BC = 8
Now,
In ΔBCD,
Applying the Pythagorean theorem,
BD² = BC² + CD²
17² = 8² + CD²
CD² = 289 - 64
CD² = 225
CD = 15
Thus,
The length of the side CD is 15.
Learn more about the Pythagorean theorem here:
https://brainly.com/question/14930619
#SPJ1
write an equivalent double intergral with the order of intergration reversed1) integral^2_0 integral^4_y^2 4y dx dyA) integral^4_0 integral^squareroot x_2 4y dy dx B) integral^4_0 integral^squareroot x_0 4y dy dx C) integral^2_0 integral^squareroot x_0 4y dy dx D) integral^2_0 integral^squareroot x_2 4y dy dx
Answers
The equivalent double integral with the order of integration reversed is:
∫4_0 ∫√(x/4)_0 4y dydx = 8/3. The correct option is B.
The given double integral is:
∫∫R 4y dxdy, where R is the region bounded by the curves x=0, x=4y^2, and y=0.
To reverse the order of integration, we need to draw the region R and express it in terms of the other variable. The region R is a triangle in the first quadrant, bounded by the x-axis, the curve y=√(x/4), and the vertical line x=4.
Therefore, the equivalent double integral with the order of integration reversed is:
∫∫R 4y dydx,
where R is the region bounded by the curves y=0, y=√(x/4), and x=4.
To evaluate this integral, we integrate with respect to y first, keeping x as a constant. The limits of integration for y are y=0 and y=√(x/4).
Therefore, the integral becomes:
∫4_0 ∫√(x/4)_0 4y dydx.
Integrating with respect to y, we get:
∫4_0 2y^2 |_0^√(x/4) dx,
which simplifies to:
∫4_0 x/2 dx = 8/3.
Therefore, the equivalent double integral with the order of integration reversed is:
∫4_0 ∫√(x/4)_0 4y dydx = 8/3.
This matches the limits of integration for the inner integral.
To know more about double integral refer here :
https://brainly.com/question/31404551#
#SPJ11
The temperature recorded by a certain thermometer when placed in boiling water (true temperature 100 degree C) is normally distributed with mean p=99.8 degree C and standard deviation sigma =1-1 degree C. a) What is the probability that the thermometer reading is greater than 100 degree C? b) What is the probability that the thermometer reading is within +- 0.05 degree C of the true temperature? c) What is the probability that a random sample of 30 thermometers has a mean thermometer reading is less than 100 degree C? (inclusive)
Answers
a) The probability that the thermometer reading is greater than 100 degree C is approximately 0.1587.
b) The probability that the thermometer reading is within +- 0.05 degree C of the true temperature is approximately 0.3830.
c) The probability that a random sample of 30 thermometers has a mean thermometer reading less than 100 degree C is approximately 0.0001.
a) Using the Z-score formula, we get Z = (100 - 99.8)/1.1 = 0.182. Looking up the standard normal distribution table, we find the probability of a Z-score being greater than 0.182 is 0.1587.
b) To find the probability that the thermometer reading is within +- 0.05 degree C of the true temperature, we need to find the area under the normal distribution curve between 99.95 and 100.05.
Using the Z-score formula for the lower and upper limits, we get Z1 = (99.95 - 99.8)/1.1 = 0.136 and Z2 = (100.05 - 99.8)/1.1 = 0.364. Looking up the standard normal distribution table for the area between Z1 and Z2, we find the probability is 0.3830.
c) The sample mean follows a normal distribution with mean 99.8 and standard deviation 1.1/sqrt(30) = 0.201. Using the Z-score formula, we get Z = (100 - 99.8)/(0.201) = 0.995. Looking up the standard normal distribution table for the area to the left of Z, we find the probability is approximately 0.0001.
For more questions like Probability click the link below:
https://brainly.com/question/30034780
#SPJ11
Water flows through circular pipe of internal diameter 3 cm at a speed of 10 cm/s. if the pipe is full, how much water flows from the pipe in one minute? (answer in litres)
Answers
Given that the water flows through a circular pipe of an internal diameter 3 cm at a speed of 10 cm/s. We are to determine the amount of water that flows from the pipe in one minute and express the answer in litres.
We can begin the solution to this problem by finding the cross-sectional area of the pipe. A = πr²A = π (d/2)²Where d is the diameter of the pipe.
Substituting the value of d = 3 cm into the formula, we obtain A = π (3/2)²= (22/7) (9/4)= 63/4 cm².
Also, the water flows at a speed of 10 cm/s. Hence, the volume of water that flows through the pipe in one second V = A × v where v is the speed of water flowing through the pipe.
Substituting the values of A = 63/4 cm² and v = 10 cm/s into the formula, we obtain V = (63/4) × 10= 630/4= 157.5 cm³. Now, we need to determine the volume of water that flows through the pipe in one minute.
There are 60 seconds in a minute. Hence, the volume of water that flows through the pipe in one minute is given by V = 157.5 × 60= 9450 cm³= 9450/1000= 9.45 litres.
Therefore, the amount of water that flows from the pipe in one minute is 9.45 litres.
Answer: The amount of water that flows from the pipe in one minute is 9.45 litres.
To know more about diameter visit:
https://brainly.com/question/4771207
#SPJ11
HeIp Rewrite the expression 0. 75 + 0. 5(d - 1) as the sum of two terms
Answers
We have expressed the given expression 0.75 + 0.5(d - 1) as the sum of two terms: 0.5d - 0.5 and 0.75.
The given expression 0.75 + 0.5(d - 1) is to be rewritten as the sum of two terms.
Let's simplify the given expression 0.75 + 0.5(d - 1) as follows:
0.75 + 0.5(d - 1)0.75 + 0.5d - 0.5
Now, we have to represent the given expression as the sum of two terms.
Hence, we have to separate the two terms using a comma:
0.5d - 0.5, 0.75
Therefore, the expression 0.75 + 0.5(d - 1) can be rewritten as the sum of two terms 0.5d - 0.5 and 0.75.
The given expression is 0.75 + 0.5(d - 1).
We are to represent this expression as the sum of two terms.
To do this, we start by simplifying the given expression by combining like terms.
0.75 + 0.5(d - 1) = 0.5d - 0.5 + 0.75
Next, we represent the expression 0.5d - 0.5 + 0.75 as the sum of two terms.
These two terms are 0.5d - 0.5 and 0.75, separated by a comma.
Therefore, we have expressed the given expression 0.75 + 0.5(d - 1) as the sum of two terms: 0.5d - 0.5 and 0.75.
To know more about expression visit:
https://brainly.com/question/28170201
#SPJ11
in exercises 24—34, determine whether each relation defined on the set of positive integers is reflexive, symmetric, antisymmetric, transitive, and/or a partial order
Answers
In order to determine if each relation is reflexive, symmetric, antisymmetric, transitive, and/or a partial order, we need to first define what each of these terms means.
- Reflexive: A relation R on a set A is reflexive if for every element a ∈ A, (a,a) ∈ R. In other words, every element is related to itself.
- Symmetric: A relation R on a set A is symmetric if for any two elements a,b ∈ A, if (a,b) ∈ R, then (b,a) ∈ R. In other words, if a is related to b, then b is related to a.
- Antisymmetric: A relation R on a set A is antisymmetric if for any two distinct elements a,b ∈ A, if (a,b) ∈ R and (b,a) ∈ R, then a = b. In other words, if a is related to b and b is related to a, then a and b are the same element.
- Transitive: A relation R on a set A is transitive if for any three elements a,b,c ∈ A, if (a,b) ∈ R and (b,c) ∈ R, then (a,c) ∈ R. In other words, if a is related to b and b is related to c, then a is related to c.
- Partial order: A relation R on a set A is a partial order if it is reflexive, antisymmetric, and transitive.
Now, we can use these definitions to analyze each relation defined on the set of positive integers from exercises 24-34. Here are the answers:
24. "a divides b" - This relation is reflexive, antisymmetric, and transitive, so it is a partial order.
25. "a is a multiple of b" - This relation is reflexive and transitive, but it is not antisymmetric, so it is not a partial order.
26. "a is less than or equal to b" - This relation is reflexive, antisymmetric, and transitive, so it is a partial order.
27. "a is greater than or equal to b" - This relation is reflexive, antisymmetric, and transitive, so it is a partial order.
28. "a is congruent to b mod 5" - This relation is reflexive, symmetric, and transitive, but it is not antisymmetric, so it is not a partial order.
29. "a is congruent to b mod 7" - This relation is reflexive, symmetric, and transitive, but it is not antisymmetric, so it is not a partial order.
30. "a is a factor of b" - This relation is reflexive, but it is not symmetric, antisymmetric, or transitive, so it is not a partial order.
31. "a is a proper factor of b" - This relation is not reflexive, symmetric, antisymmetric, or transitive, so it is not a partial order.
32. "a and b have the same prime factorization" - This relation is reflexive, symmetric, and transitive, but it is not antisymmetric, so it is not a partial order.
33. "a and b have the same number of prime factors" - This relation is reflexive, symmetric, and transitive, but it is not antisymmetric, so it is not a partial order.
34. "a and b have no common factors other than 1" - This relation is reflexive, symmetric, and transitive, but it is not antisymmetric, so it is not a partial order.
Learn more about symmetric
brainly.com/question/30011125
#SPJ11
Simplify (3+√2)(3-√2).
Answers
Answer:
7
Step-by-step explanation:
Formula
(a + b) (a - b) = a² - b²
Here
a = 3
b = √2
(3 + √2) (3 - √2)
= 3² - (√2)²
= 9 - 2
= 7
Sam is building a cutlery holder for his wife.he wants to slope to be 0.7 calculate the height of each vertical column, labeled 'a', 'b', 'c','d','e'
Answers
In order to build a cutlery holder with a slope of 0.7, Sam needs to determine the height of each vertical column, labeled 'a', 'b', 'c', 'd', and 'e'. Sam will be able to create a cutlery holder with a slope of 0.7.
To calculate the height of each vertical column, Sam needs to understand the concept of slope. Slope is the ratio of the vertical change (rise) to the horizontal change (run). In this case, the slope is given as 0.7.
Let's assume that the horizontal distance between each column is equal. We can assign a standard value of 1 unit for the horizontal run between columns.
To find the vertical rise for each column, we can multiply the horizontal run by the slope. Therefore, the height of column 'a' would be 0.7 units, column 'b' would be 1.4 units (0.7 * 2), column 'c' would be 2.1 units (0.7 * 3), column 'd' would be 2.8 units (0.7 * 4), and column 'e' would be 3.5 units (0.7 * 5).
By assigning these respective heights to each vertical column, Sam will be able to create a cutlery holder with a slope of 0.7.
Learn more about slope here:
https://brainly.com/question/3605446
#SPJ11
Help me fix this (image attached)
Answers
The value of x from given quadrilateral ABCD is 27°.
In the given quadrilateral ABCD, ∠A=3x+5, ∠B=2x+15, ∠C=4x and ∠D=4x-10.
We know that, the sum of interior angles of quadrilateral is 360°.
Here, ∠A+∠B+∠C+∠D=360°
3x+5+2x+15+4x+4x-10=360°
13x+10=360°
13x=350°
x=350/13
x=26.9
x≈27°
Therefore, the value of x from given quadrilateral ABCD is 27°.
Learn more about the quadrilaterals here:
https://brainly.com/question/29934440.
#SPJ1
Consider the following vectors: v1 = 1 2 1 ; v2 = 1 3 2 ; v3 = 1 0 4 ; (a) Determine if these vectors are linearly independent or dependent. (b) Is is possible to express v = 1 2 −3 as a linear combination of v1, v2, and v3?
Answers
By solving the system of equations, we find that there is no solution. Therefore, it is not possible to express v = [1 2 -3] as a linear combination of v1, v2, and v3.
(a) To determine if the vectors v1, v2, and v3 are linearly independent or dependent, we can form a matrix A by placing the vectors as columns:
A = [v1 v2 v3]
| 1 1 1 |
| 2 3 0 |
| 1 2 4 |
Next, we can perform row operations to check if the matrix A is row equivalent to the identity matrix. If we can row reduce A to the identity matrix, then the vectors are linearly independent. Otherwise, they are linearly dependent.
Performing row operations on matrix A, we can obtain the following row-echelon form:
| 1 1 1 |
| 0 1 -2 |
| 0 0 0 |
Since there is a row of zeros in the row-echelon form, we can conclude that the vectors v1, v2, and v3 are linearly dependent.
(b) To determine if it is possible to express v = [1 2 -3] as a linear combination of v1, v2, and v3, we can set up the equation:
x1v1 + x2v2 + x3*v3 = v
This leads to the system of equations:
x1 + x2 + x3 = 1
2x1 + 3x2 + 2x3 = 2
x1 + 2x2 + 4x3 = -3
We can solve this system of equations using various methods such as Gaussian elimination or matrix inversion. After solving the system, if there exists a solution for x1, x2, and x3, then it is possible to express v as a linear combination of v1, v2, and v3. Otherwise, it is not possible.
Know more about system of equations here:
https://brainly.com/question/12895249
#SPJ11
given x=45.5, μ=40, and σ=2, indicate on the curve where the given x value would be.
Answers
The exact position of x=45.5 can be indicated on this curve using the corresponding z-score.
Assuming a normal distribution with mean μ=40 and standard deviation σ=2, we can use the standard normal distribution curve to determine the position of x=45.5.
First, we calculate the z-score of x=45.5 using the formula:
z = (x - μ) / σ
Substituting the given values, we get:
z = (45.5 - 40) / 2
z = 2.75
This means that x=45.5 is 2.75 standard deviations above the mean.
A standard normal distribution table or a calculator to find the area under the curve to the left of z=2.75.
This area represents the proportion of values that are less than or equal to z=2.75.
Using a calculator, we find that the area to the left of z=2.75 is approximately 0.997.
This means that about 99.7% of values in a normal distribution are less than or equal to x=45.5.
On the standard normal distribution curve, the value of z=2.75 is located to the right of the mean, and the area under the curve to the left of z=2.75 is shaded.
For similar questions on curve
https://brainly.com/question/31012623
#SPJ11
The given x value of x = 45.5 falls to the right of the mean (μ) on the normal distribution curve.
In a normal distribution, the mean (μ) represents the center of the distribution, and the standard deviation (σ) determines the spread of the data. The normal distribution is symmetric, so values to the left of the mean are smaller, while values to the right are larger.
Given x = 45.5, which is greater than the mean μ = 40, we can infer that the corresponding point on the normal distribution curve would be to the right of the mean. The exact location of x = 45.5 on the curve would depend on the standard deviation σ.
The standard deviation σ = 2 provides information about how the data is spread around the mean. However, without further information, we cannot determine the specific position of x = 45.5 on the curve relative to the standard deviation.
To learn more about standard deviation click here
brainly.com/question/29115611
#SPJ11
T/f the p-value is the proportion of samples, when the null hypothesis is true, that would give a statistic as extreme as (or more extreme than) the observed sample.
Answers
True. The p-value is defined as the probability of obtaining a statistic as extreme as (or more extreme than) the observed sample, assuming that the null hypothesis is true.
It is essentially a measure of evidence against the null hypothesis and is used to assess the significance of a particular statistical result. The p-value is typically compared to a predetermined level of significance, known as the alpha level, to determine whether to reject or fail to reject the null hypothesis.
It is important to note that the p-value is not the same as the proportion of samples that would give a statistic as extreme as the observed sample. Rather, it is the probability of obtaining such a statistic, given that the null hypothesis is true. The proportion of samples that would give a similar statistic is known as the sampling distribution, which is a theoretical distribution that describes the range of possible values for a statistic, assuming that the null hypothesis is true.
In summary, the p-value provides a measure of the strength of evidence against the null hypothesis, while the sampling distribution describes the range of possible values for a statistic under the null hypothesis. Together, these concepts form the basis of hypothesis testing and are essential for making informed decisions based on statistical data.
Learn more about null hypothesis here:
https://brainly.com/question/28920252
#SPJ11
solve the initial value problem: dr dt + 2tr = r, r(0) = 5.
Answers
So the solution to the initial value problem is: r = 5e^(2t) - t^2.
To solve the initial value problem:
dr/dt + 2tr = r, r(0) = 5,
we can use an integrating factor.
First, we can rewrite the equation as:
dr/dt - r = -2tr
The integrating factor is e^(-2t). We can multiply both sides of the equation by e^(-2t) to obtain:
e^(-2t)dr/dt - e^(-2t)r = -2te^(-2t)r
We can rewrite the left-hand side using the product rule:
(d/dr)(e^(-2t)r) = -2te^(-2t)r
Integrating both sides with respect to r, we get:
e^(-2t)r = -e^(-2t)t^2 + C
where C is the constant of integration.
Solving for r, we get:
r = Ce^(2t) - t^2
Using the initial condition r(0) = 5, we get:
5 = C(1) - 0
C = 5
To know more about initial value problem,
https://brainly.com/question/30782698
#SPJ11
Justin wraps a gift box in the shape of a right rectangular prism. The figure below shows a net for the gift box.
Answers
Justin wants 654 cm² wrapping paper for wrap the gift.
Given that;
Justin wraps a gift box in the shape of a right rectangular prism.
Now, We get;
According to the wrapping paper, we can get cuboid,
The surface area is,
= 2 [ (length x width ) + width x height + height x length]
= 2 [ 15 x 8 + 8 x 9 + 9 x 15 ]
= 2 [120 + 72 + 135]
= 654 cm²
Thus, Justin wants 654 cm² wrapping paper for wrap the gift.
Learn more about the cuboid visit:
https://brainly.com/question/26403859
#SPJ1
The number of CDs per hour that Snappy Hardware can manufacture at its plant is given by P=064 where x is the number of workers at the plant and y is the monthly budget in dollars. Assuming that P is constant.compute dy/d when w100 and y 120,000, Coninuing with the previous problem,give an interpretation in 3 parts of the value you computed in terms of CDs produced by Snoppy Hardware.
Answers
The value of dy/d in this case represents the rate of change in the monthly budget required to maintain a constant production level of CDs.
When w100 and y 120,000, dy/d can be computed by taking the partial derivative of the given equation with respect to y: dy/d = -0.64/x. Plugging in the given values, we get dy/d = -0.0064.
1. If the monthly budget is increased by $1, Snappy Hardware can manufacture 0.0064 fewer CDs per hour while maintaining the same number of workers.
2. If the number of workers is increased by 1, Snappy Hardware can manufacture an additional 0.0064 CDs per hour while maintaining the same monthly budget.
3. If Snappy Hardware wants to maintain a constant production level of CDs, they need to decrease their monthly budget by $156,250 for every 10,000 CDs they want to produce per hour.
To know more about partial derivative click on below link:
https://brainly.com/question/31397807#
#SPJ11
The test statistic of z equals 2.45 is obtained when testing the claim that p not equals 0.449. a. Identify the hypothesis test as being two-tailed, left-tailed, or right-tailed. b. Find theP-value. c. Using a significance level of alphaequals 0.10, should we reject Upper H 0 or should we fail to reject Upper H 0?
Answers
The hypothesis test is two-tailed.
The P-value is the probability of obtaining a test statistic as extreme as the observed value (or even more extreme) under the null hypothesis. In this case, with a two-tailed test, we need to find the probability in both tails of the distribution. To find the P-value, we compare the test statistic to the critical values of the standard normal distribution. The P-value is the probability of observing a test statistic as extreme as 2.45 or more extreme in both directions.
Using a significance level of alpha equals 0.10, we compare the P-value to the significance level. If the P-value is less than the significance level, we reject the null hypothesis. If the P-value is greater than or equal to the significance level, we fail to reject the null hypothesis. In this case, if the P-value is less than 0.10, we reject the null hypothesis. If the P-value is greater than or equal to 0.10, we fail to reject the null hypothesis.
Know more about hypothesis here:
https://brainly.com/question/29519577
#SPJ11
continuing with the previous problem, find the equation of the tangent line to the function at the point (2, f (2)) = (2, 4) . show work and give tangent line in the form y = mx b .
Answers
The required answer is the equation of the tangent line to the function at the point (2, f(2)) = (2, 4) is y = 6x - 8.
To find the equation of the tangent line to the function at the point (2, f(2)) = (2, 4), we need to first find the derivative of the function at x = 2.
Assuming we have the original function loaded in content, we can find the derivative as follows:
f(x) = x^2 + 2x
f'(x) = 2x + 2
The tangent line touched the a curve can be made more explicit by considering the sequence of straight lines passing through two points, A and B, those that lie on the function curve. The tangent at is the limit when points ,approximates or tends .
If two circular arcs meet at a sharp point then there is no uniquely defined tangent at the vertex because the limit of the progression of secant lines depends on the direction in which "point B" approaches the vertex.
The existence and uniqueness of the tangent line depends on a certain type of mathematical smoothness, known as "differentiability."
Now we can plug in x = 2 to find the slope of the tangent line at that point:
f'(2) = 2(2) + 2 = 6
So the slope of the tangent line is m = 6.
To find the y-intercept (b) of the tangent line, we can use the point-slope form of a line:
y - y1 = m(x - x1)
Plugging in the point (2, 4) and the slope we just found, we get:
y - 4 = 6(x - 2)
Simplifying and solving for y, we get the equation of the tangent line in slope-intercept form:
y = 6x - 8
Therefore, the equation of the tangent line to the function at the point (2, f(2)) = (2, 4) is y = 6x - 8.
To know more about the tangent line . Click on the link.
https://brainly.com/question/12648495
#SPJ11
PLEASE DO THIS QUICK MY TIME IS RUNNING OUT
Answers
Answer:
c
Step-by-step explanation:
a = probably 90°
b = 180°
c = probably less than 90°
d = probably more than 90° ( > 90°)
#CMIIWAnswer:
c
Step-by-step explanation:
Ais 90 degrees
B is 180
C is less than 90, looks around 45 so 51 isnt that far off
D is between 90 and 180
Determine whether the geometric series is convergent or divergent 9 n=1 convergent divergent If it is convergent, find its sum. (If the quantity diverges, enter DIVERGES.)
Answers
The geometric series 9^n=1 is divergent because as n increases, the terms of the series get larger and larger without bound. Specifically, each term is 9 times the previous term, so the series grows exponentially.
To see this, note that the first few terms are 9, 81, 729, 6561, and so on, which clearly grow without bound. Therefore, the sum of this series cannot be determined since it diverges. In general, a geometric series with a common ratio r is convergent if and only if |r| < 1, in which case its sum is given by the formula S = a/(1-r), where a is the first term of the series.
However, if |r| ≥ 1, then the series diverges. In the case of 9^n=1, the common ratio is 9, which is clearly greater than 1, so the series diverges.
To know more about geometric series refer to
https://brainly.com/question/4617980
#SPJ11
The Alton Company produces metal belts. During the current month, the company incurred the following product costs:
Answers
According to the information, the Alton Company's total product costs amount to $156,500.
How to calculate the total product costs?Explanation: To calculate the total product costs, we need to sum up the various cost components incurred by the company:
Raw materials: $81,000Direct labor: $50,500Electricity used in the Factory: $20,500Factory foreperson salary: $2,650Maintenance of factory machinery: $1,850Adding all these costs together, we get:
$81,000 + $50,500 + $20,500 + $2,650 + $1,850 = $156,500
According to the above we can infer that the correct answer is $156,500.
Note: This question is incomplete. Here is the complete information:
Alton Company produces metal belts.
During the current month, the company incurred the following product costs: Raw materials $81,000; Direct labor $50,500; Electricity used in the Factory $20,500; Factory foreperson salary $2,650; and Maintenance of factory machinery $1,850. Alton Company's total product costs:
$23,150.$131,500.$25,000.$156,500.Note: This question is incomplete; here is the complete question:
Alton Company produces metal belts.
During the current month, the company incurred the following product costs: Raw materials $81,000; Direct labor $50,500; Electricity used in the Factory $20,500; Factory foreperson salary $2,650; and Maintenance of factory machinery $1,850. Alton Company's total product costs:
Multiple Choice
$23,150.
$131,500.
$25,000.
$156,500.
Learn more about costs in: https://brainly.com/question/14725550
#SPJ4
Find average speed of car in km/h given that it took 2 hours 15 minutes to travel 198 km
Answers
The average speed of the car was 88 km/h.
To find the average speed of a car, we need to use the formula `average speed = total distance ÷ total time`.In this case, the car traveled a total distance of 198 km and it took 2 hours and 15 minutes to travel that distance. We need to convert the time to hours.1 hour = 60 minutes, so 2 hours 15 minutes = 2 + 15/60 hours = 2.25 hours .
Now we can use the formula to find the average speed of the car:average speed = total distance ÷ total time average speed = 198 km ÷ 2.25 hours average speed = 88 km/h Therefore, the average speed of the car was 88 km/h.
Learn more about distance here,
https://brainly.com/question/26550516
#SPJ11
Gloria and Brad each left the same building at the same time to drive home in the same
direction. Gloria traveled at a rate of 54 mph and Brad's rate was 42 mph. In how many
hours were they 54 miles apart?
3.5 hours
4 hours
B
4.5 hours
3 hours
Answers
After 4.5 hours of travel, they will be 54 miles apart.
Let's assume that t is the time (in hours) they have been traveling.
The distance traveled by Gloria can be calculated as 54t (54 miles per hour multiplied by t hours), and the distance traveled by Brad can be calculated as 42t (42 miles per hour multiplied by t hours).
To find the time at which they are 54 miles apart, we need to solve the equation:
54t - 42t = 54
Simplifying the equation:
12t = 54
Dividing both sides by 12:
t = 4.5
Therefore, they will be 54 miles apart after 4.5 hours of traveling.
Learn more about expression here:
https://brainly.com/question/14083225
#SPJ1
Find the surface area of the cylinder. Round your answer to the nearest tenth.
about
cm
3 cm
cm²
Answers
Answer:
62.8
Step-by-step explanation
The random variable for a chi-square distribution may assume a. any value between-1 to b. any value infinity to +infinity c. any negative value d. Any tive value
Answers
The random variable for a chi-square distribution may assume:
d. Any positive value
Because, A chi-square distribution is used to analyze the variability of observed data and has only non-negative values.
Since it measures the squared differences between observed and expected values, it cannot have negative values.
So, the random variable for a chi-square distribution can assume any positive value, including zero.
The chi-square distribution is a probability distribution that arises in statistics and is used in hypothesis testing and confidence interval calculations.
It is the distribution of the sum of squares of independent standard normal random variables.
The degree of freedom parameter specifies the number of independent standard normal random variables being summed.
The chi-square distribution is often used to test the goodness-of-fit of an observed frequency distribution to an expected theoretical distribution, and to test the independence of two categorical variables in a contingency table.
It is a non-negative, right-skewed distribution with an expected value equal to the degrees of freedom and a variance equal to twice the degrees of freedom.
d. Any positive value is correct.
For similar question on chi-square distribution.
https://brainly.com/question/4543358
#SPJ11
The correct answer is (b) any value from zero to positive infinity. A chi-square distribution is a probability distribution that takes only non-negative values. It is often used in hypothesis testing to determine the goodness of fit between observed data and theoretical distributions.
The distribution is characterized by its degrees of freedom, which determines the shape of the distribution. The greater the degrees of freedom, the closer the distribution approximates a normal distribution. The chi-square distribution is widely used in statistics and is particularly useful in the analysis of categorical data. The properties of the chi-square distribution make it a useful tool in statistical analysis. Its non-negativity property makes it suitable for modeling data that cannot be negative, such as the number of people in a given population. The distribution also has a number of desirable properties that make it easy to work with, such as its additivity property. This allows for the construction of statistical tests that can be used to determine the significance of observed differences between data sets. Overall, the chi-square distribution is an important tool in statistical analysis that has many applications in various fields, including finance, biology, and engineering.
Learn more about chi-square distribution here: brainly.com/question/31959177
#SPJ11
Given a pure renewal process {N(t) : t ≥ 0} and the cdf F(·) of ξ1, derive the renewal-type equation for H(t) := m(t) = E[N(t)]. In other words, determine the function D(t) such that the renewal-type equation holds.
Answers
Let ξ1, ξ2, ξ3, ... be the interarrival times of the pure renewal process {N(t) : t ≥ 0}.
Then, the renewal-type equation for the expected number of arrivals up to time t, denoted by H(t) or m(t), is given by:
H(t) = E[N(t)] = E[1 + N(t − ξ1)] = 1 + E[N(t − ξ1)]
The last equality follows from the memoryless property of the exponential distribution, which implies that N(t − ξ1) has the same distribution as N(t), shifted by a time of ξ1.
Let F(x) be the cumulative distribution function (cdf) of ξ1, and let f(x) = F'(x) be its probability density function (pdf). Then, we have:
H(t) = 1 + ∫_0^t H(t − x) f(x) dx
This is the renewal-type equation for H(t) or m(t), with the function D(t) = f(t). The interpretation of this equation is that the expected number of arrivals up to time t is the sum of the first arrival (which occurs with probability 1) and the expected number of arrivals up to time t − ξ1, weighted by the probability density of ξ1.
The integral term represents the expected number of arrivals up to time t − x, given that the first arrival occurred at time x, and is weighted by the probability density of the interarrival time x.
To know more about renewal process refer here:
https://brainly.com/question/15562081?#
#SPJ11
Select all expressions that are squares of linear expressions (perfect squares).
Answers
To identify the perfect squares among the given expressions, we need to determine which ones can be written as the square of a linear expression.
A perfect square is a result of squaring a linear expression, where a linear expression is of the form ax + b, where a and b are constants. When we square a linear expression, we obtain a quadratic expression.
To determine if an expression is a perfect square, we can expand it and check if it can be factored into the square of a linear expression. If it can be factored in this way, then it is a perfect square.
Let's examine each expression:
1. (x + 3)(x + 3) = [tex]x^2[/tex] + 6x + 9: This expression can be factored into the square of (x + 3), so it is a perfect square.
2. (2x - 1)(2x - 1) = 4[tex]x^2[/tex] - 4x + 1: This expression can be factored into the square of (2x - 1), so it is a perfect square.
3. (3x + 4)(3x + 4) = 9[tex]x^2[/tex] + 24x + 16: This expression can be factored into the square of (3x + 4), so it is a perfect square.
4. (x - 5)(x + 5) = [tex]x^2[/tex] - 25: This expression is not a perfect square because it cannot be factored into the square of a linear expression.
Therefore, the expressions that are perfect squares are: (x + 3)(x + 3), (2x - 1)(2x - 1), and (3x + 4)(3x + 4).
Learn more about linear expression here:
https://brainly.com/question/30111963
#SPJ11
Which equation is true? 10 + (7 − 3) ÷ 2 = (10 + 4) ÷ 2 10 + (7 − 3) ÷ 2 = 4 + 1.5 × 2 10 + (7 − 3) ÷ 2 = 2 × 6 − 1.5 10 + (7 − 3) ÷ 2 = 8 × 3 ÷ 2
Answers
The true equation from the list of options is 10 + (7 − 3) ÷ 2 = 8 × 3 ÷ 2
Selecting the true equationFrom the question, we have the following parameters that can be used in our computation:
The list of options
Next, we evaluate the equations to test which is true
Using the above as a guide, we have the following:
10 + (7 − 3) ÷ 2 = (10 + 4) ÷ 2
12 = 7 --- false
10 + (7 − 3) ÷ 2 = 4 + 1.5 × 2
12 = 7 --- false
10 + (7 − 3) ÷ 2 = 2 × 6 − 1.5
12 = 10.5 --- false
10 + (7 − 3) ÷ 2 = 8 × 3 ÷ 2
12 = 12
Hence, the true equation is 10 + (7 − 3) ÷ 2 = 8 × 3 ÷ 2
Read more about equivalent expressions at
https://brainly.com/question/2972832
#SPJ1
suppose that x is a discrete random variable following a geometric distribution, where suppose n observations are obtained independently from this distribution
Answers
Given that x is a discrete random variable following a geometric distribution, and n observations are obtained independently from this distribution, we can use these observations to study the properties of the geometric distribution and make statistical inferences.
The geometric distribution models the probability of the number of trials needed to obtain the first success in a sequence of independent Bernoulli trials, where each trial has a constant probability of success, denoted by p.
By obtaining n independent observations from this distribution, we can estimate the probability of success (p) and analyze various properties such as the mean, variance, and probability mass function of the geometric distribution. These statistical properties can provide insights into the behavior of the random variable x and can be used for further analysis, prediction, or decision-making.
Furthermore, with the observed data, we can conduct hypothesis tests, construct confidence intervals, or perform other statistical analyses to make inferences about the underlying geometric distribution and its parameters.
Learn more about geometric distribution here: brainly.com/question/29210110
#SPJ11
Consider the equation. Select the operation needed to perform each step.
36 = 16 - 10m
Step 1: To isolate the term with the variable.
Choices: Add 16 to both sides.
Add 10m to both sides.
Subtract 16 from both sides.
Subtract 10m from both sides.
Multiply both sides by 10.
Divide both sides by 10.
Step 2: To Isolate the variable.
Choices: Add 16 to both sides.
Add 10m to both sides.
Subtract 16 from both sides.
Subtract 10m from both sides.
Multiply both sides by -10.
Divide both sides by -10.
Step 3: Solve for m.
Answers
The value of m for the expression will be m = -2.
In mathematics, an expression is a combination of one or more numbers, variables, constants, and operators, which when evaluated, produce a value.
Expressions can include mathematical symbols such as addition, subtraction, multiplication, division, exponents, roots, logarithms, and trigonometric functions.
To isolate the term with the variable. Subtract 16 from both sides.
36 - 16 = -10m
20 = -10m
To isolate the variable.
Divide both sides by -10.
20 / (-10) = m
0-2 = m
Solve for m.
The solution is m = -2.
To know more about an expression follow
https://brainly.com/question/1859113
#SPJ1