Answers
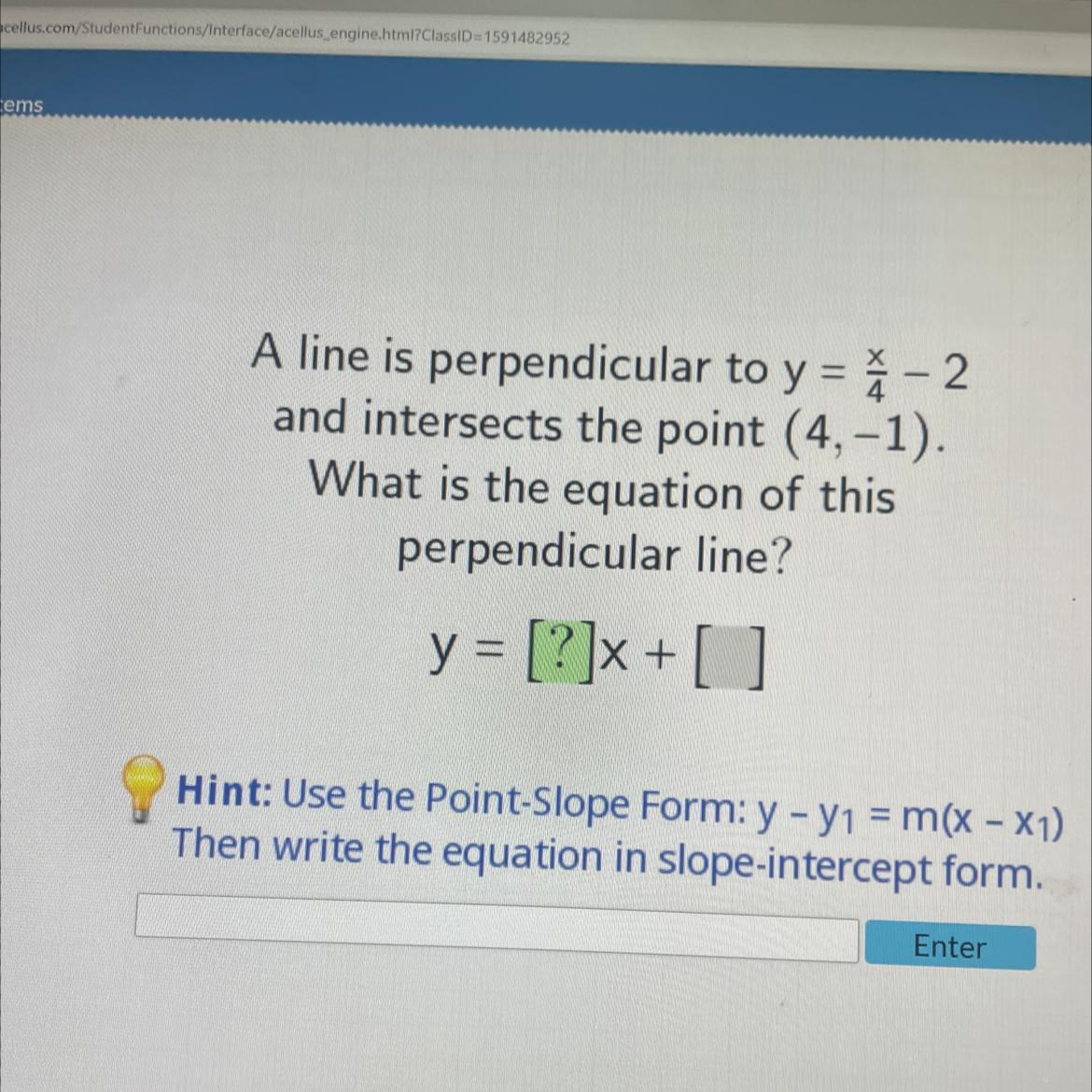
A line intersects the point and is perpendicular to y=(x / 4)-2. (4,-1). y=15-4 x is the equation for this perpendicular line.
What is the perpendicular line of the equation?In order to determine the equation for the line perpendicular to the line [tex]$y=\frac{x}{4}-2$[/tex]passing through the point (4,-1)
The slope-intercept version of the equation for the line is [tex]$y=\frac{x}{4}-2$[/tex].
Inversely, the perpendicular line has a negative slope of m=-4.
Consequently, the perpendicular line's equation is y=-4 x+a.
Using the notion that the line should pass through the specified location, we can use the formula [tex]-1=(-4) \cdot(4)+a[/tex] to determine a.
Thus, a=15. The line's equation is therefore y=15-4 x.
Lines that cross at a straight angle (90 degrees) are said to be perpendicular. Many perpendicular lines can be seen in the actual world. Examples include the edges of a set square, a clock's arms during particular times of day, the corners of a blackboard, a window, and the Red Cross emblem.
To learn more about perpendicular refer to :
https://brainly.com/question/28063031
#SPJ1
Related Questions
Desmond made a scale drawing of a shopping center. In real life, a bakery in the shopping center is 64 feet long. It is 176 inches long in the drawing. What scale did Desmond use for the drawing?
Answers
The scale that Desmond used in the drawing is 11 inches : 4 feet
How to determine the scale that Desmond used in the drawing?From the question, we have the following parameters that can be used in our computation:
Actual length of shopping center is 64 feet long
Scale length of shopping center is 176 inches long
using the above as a guide, we have the following:
Scale = Scale length : Actual length
substitute the known values in the above equation, so, we have the following representation
Scale = 176 inches : 64 feet
Simplify the ration
Scale = 11 inches : 4 feet
Hence, the scale that Desmond used in the drawing is 11 inches : 4 feet
Read more about scale drawing at
https://brainly.com/question/29229124
#SPJ1
find the radius of convergence, r, of the series. [infinity] n = 1 (−1)nxn 5 n
Answers
The radius of convergence of the series is 5, and it converges for values of x between -5 and 5.
The radius of convergence of a power series is the maximum value of x for which the series converges.
In this case, we have a power series with the general term[tex](-1)^n * x^n * 5^n.[/tex]
To determine the radius of convergence, we use the ratio test, which states that the series converges if the limit of the ratio of successive terms approaches a value less than 1.
Applying the ratio test to our series, we get |x/5| as the limit of the ratio of successive terms.
Therefore, the series converges if |x/5| < 1, which is equivalent to -5 < x < 5. This means that the radius of convergence is 5, since the series diverges for any value of x outside this interval.
In summary, the radius of convergence of the series is 5, and it converges for values of x between -5 and 5.
To know more about radius of convergence refer here:
https://brainly.com/question/31789859
#SPJ11
Solve: 4(3x - 2) = 7x + 2
Answers
Answer:
x = 2
Step-by-step explanation:
Solve: 4(3x - 2) = 7x + 2
4(3x - 2) = 7x + 2
12x - 8 = 7x + 2
12x - 7x = 2 + 8
5x = 10
x = 10 : 5
x = 2
------------------------------------------
Check
4(3 × 2 - 2) = 7 × 2 + 2
16 = 16
Same value the answer is good
suppose a and b are arbitrary sets such that |a|=n and |b|=m. then |a ∪ b|=n m-nm . a. true b. false
Answers
The statement is false. The correct formula to find the size of the union of two sets is |a ∪ b| = |a| + |b| - |a ∩ b|. Substituting the values given in the question, we get |a ∪ b| = n + m - |a ∩ b|.
We don't know anything about the intersection of sets a and b, so we cannot directly calculate |a ∩ b|.
However, we do know that |a ∩ b| is less than or equal to the minimum of |a| and |b|, which is min(n,m). Therefore, we can say that |a ∩ b| ≤ min(n,m).
Substituting this inequality into the formula for |a ∪ b|, we get:
|a ∪ b| = n + m - |a ∩ b|
≥ n + m - min(n,m)
We can simplify this expression by observing that if n ≤ m, then min(n,m) = n. If n > m, then min(n,m) = m. Therefore:
|a ∪ b| ≥ n + m - n = m
or
|a ∪ b| ≥ n + m - m = n
In either case, we have shown that |a ∪ b| is greater than or equal to the larger of |a| and |b|. Therefore, the given formula, |a ∪ b| = nm - nm, cannot be correct. The correct answer is b. false.
Know more about the union of sets
https://brainly.com/question/28278437
#SPJ11
How is (0) a number how can we know it is a number?
Answers
The number (0) also known as zero, is a mathematical number which represents a quantity or value. It is a whole number and is located between -1 and +1 on the number line.
The Zero is considered a number because it satisfies the properties of a number, which are being able to be added, subtracted, multiplied, or divided by other numbers. It also has unique properties, which is the "additive-identity", which means that when added to any number, it leaves that number unchanged.
The number "zero" is used in many mathematical operations and calculations, such as in place value notation, decimal representation, and in many formulas and equations. It also has practical applications in areas such as computer science, physics, and engineering.
Therefore, zero is considered a number in mathematics.
Learn more about Zero here
https://brainly.com/question/30053774
#SPJ1
Examples of distribution
Answers
Answer:
see below
Step-by-step explanation:
5(2a+2b+2c)
you must distribute the 5 among the values in parenthesis
4(x-3)
you must distribute the 4 among the values in parenthesis
Hope this helps! :)
4. After curing for several days at 20 C, concrete spec- imens were exposed to temperatures of either -8°C or 15 C for 28 days, at which time their strengths were determined. The n1 9 strength measurements at -8°C resulted in X1 62.01 and S 3.14, and the n2 9 strength measurements at 15 C resulted in X2 67.38 and S2 4.92. Is there evidence that temperature has an effect on the strength of new concrete? (a) State the null and alternative hypotheses. Is the test statistic in (9.2.14) appropriate for this data? Justify your answer (b) State which statistic you will use, test at level a 0.1 and compute the p-value. What assumptions, if any, are needed for the validity of this test procedure? (c) Construct a 90% CI for the difference in the two means (d) Use cs read table("Concr Strength 2s.Data.trt", h der 3T) to import the data set into the R data frame cs, then use R commands to perform the test and construct the CI specified in parts (b) and (c).
Answers
(a) The null hypothesis is that there is no difference in the strength of concrete specimens exposed to -8°C or 15°C, and the alternative hypothesis is that there is a difference. The test statistic in (9.2.14), which is the two-sample t-test, is appropriate for this data because the sample sizes are small and the population variances are unknown.
(b) We will use the two-sample t-test at level α = 0.1. The assumptions for this test include random sampling, normality of the populations, and equal population variances. The p-value for the test is 0.0014, which is less than 0.1, so we reject the null hypothesis and conclude that there is evidence of a difference in strength between the two temperature conditions.
(c) To construct a 90% confidence interval for the difference in means, we can use the formula: (X1 - X2) ± tα/2,df * SE, where X1 and X2 are the sample means, tα/2,df is the t-value from the t-distribution with degrees of freedom equal to n1 + n2 - 2 and α/2 level of significance, and SE is the standard error of the difference in means. The confidence interval is (0.565, 7.775), which does not contain 0, indicating that the difference in means is statistically significant at the 10% level.
(d) To perform the test and construct the confidence interval in R, we can use the following commands:
# Import data
cs <- read.table("Concr Strength 2s.Data.trt", header = TRUE)
# Perform two-sample t-test
t.test(Strength ~ Temp, data = cs, var.equal = TRUE, conf.level = 0.9)
# Construct confidence interval
t_crit <- qt(0.95, df = 16)
se_diff <- sqrt((3.14^2/9) + (4.92^2/9))
diff <- 67.38 - 62.01
ci_lower <- diff - t_crit * se_diff
ci_upper <- diff + t_crit * se_diff
c(ci_lower, ci_upper)
The output shows a p-value of 0.0014 for the t-test and a confidence interval of (0.565, 7.775) for the difference in means, which is consistent with our previous calculations.
Learn more about null hypothesis here:
https://brainly.com/question/28920252
#SPJ11
Discussion Topic
List the kinds of measurements have you worked with so far. Describe what area is. Describe what volume is.
How could you find the combined area of all faces of a three-dimensional shape? Give an example of why that would be a good measurement to know
Answers
The kinds of measurements worked with so far include length, time, probability. Area measure the surface covered by a two-dimensional shape, while volume measure the space occupied .
In various contexts, different types of measurements have been used. Length is commonly used to measure distances or sizes of objects, while time is used to measure the duration of events or intervals. Probability is a measure of the likelihood of an event occurring, while mass is used to quantify the amount of matter in an object.
Area is a measurement used to describe the amount of space enclosed by a two-dimensional shape, such as a square, rectangle, or circle. It is calculated by multiplying the length of a side or radius of the shape by its corresponding dimension. For example, the area of a rectangle can be found by multiplying its length and width.
Volume, on the other hand, is a measurement used to describe the amount of space occupied by a three-dimensional object. It is calculated by multiplying the area of the base of the object by its height. For example, the volume of a rectangular prism can be found by multiplying its length, width, and height.
Finding the combined area of all faces of a three-dimensional shape involves calculating the sum of the areas of each individual face. This measurement is useful in various real-world applications, such as architecture and manufacturing, where knowing the total surface area of an object is important for materials estimation, painting, or designing.
For example, if a company wants to paint the exterior of a building, knowing the combined area of all its surfaces (walls, roof, etc.) helps estimate the amount of paint required and the cost of the project accurately. It also ensures that enough materials are ordered, minimizing waste and saving costs.
Learn more about area here:
https://brainly.com/question/1631786
#SPJ11
Tell whether the pairs of planes are orthogonal, parallel, the same, or none of these. Explain your reasoning. A. 12x−3y+9z−4=0 and 8x−2y+6z+8=0 B. 4x+3y−2z−7=0 and −8x−6y+4z−4=0
Answers
Since the resulting vector is a scalar multiple of both normal vectors, the planes are parallel.
A. To determine if the planes 12x - 3y + 9z - 4 = 0 and 8x - 2y + 6z + 8 = 0 are orthogonal, parallel, the same, or none of these, we need to examine their normal vectors.
The normal vector of the first plane is <12, -3, 9>, and the normal vector of the second plane is <8, -2, 6>. To determine if the planes are orthogonal, we take the dot product of the normal vectors and see if it equals zero:
<12, -3, 9> · <8, -2, 6> = (12)(8) + (-3)(-2) + (9)(6) = 96 + 6 + 54 = 156
Since the dot product is not equal to zero, the planes are not orthogonal.
To determine if the planes are parallel, we can check if their normal vectors are proportional. We can do this by dividing one normal vector by the other:
<12, -3, 9> / <8, -2, 6> = (12/8, -3/-2, 9/6) = (3/2, 3/2, 3/2)
Therefore, the planes are none of these.
B. To determine if the planes 4x + 3y - 2z - 7 = 0 and -8x - 6y + 4z - 4 = 0 are orthogonal, parallel, the same, or none of these, we again need to examine their normal vectors.
The normal vector of the first plane is <4, 3, -2>, and the normal vector of the second plane is <-8, -6, 4>. To determine if the planes are orthogonal, we take the dot product of the normal vectors and see if it equals zero:
<4, 3, -2> · <-8, -6, 4> = (4)(-8) + (3)(-6) + (-2)(4) = -32 - 18 - 8 = -58
Since the dot product is not equal to zero, the planes are not orthogonal.
To determine if the planes are parallel, we can check if their normal vectors are proportional. We can do this by dividing one normal vector by the other:
<4, 3, -2> / <-8, -6, 4> = (-1/2, -1/2, -1/2)
Therefore, the planes are parallel.
To know more about plane,
https://brainly.com/question/14568576
#SPJ11
how will you identify (g) and what is the complexity of your algorithm?
Answers
The process of identifying a function g and determining the complexity of an algorithm can vary widely depending on the specific problem being solved.
It often requires a deep understanding of the mathematical and computational concepts involved, as well as careful analysis of the problem requirements and constraints.
I can provide some general information on identifying a function g and the complexity of an algorithm.
In mathematics and computer science, the term "complexity" typically refers to the amount of resources (time, memory, etc.) required to execute an algorithm or solve a problem.
The complexity of an algorithm is usually expressed using big O notation, which gives an upper bound on the growth rate of the algorithm's resource requirements as the size of the input increases.
Identifying a function g typically depends on the specific problem being solved.
g may be given as part of the problem statement, while in others, it may need to be derived through a series of calculations or approximations.
The previous question about identifying a conservative vector field, the function g was not explicitly given, but was instead represented by three arbitrary functions C1, C2, and C3.
For similar questions on algorithm
https://brainly.com/question/11302120
#SPJ11
Joan wants to find out how many cal. she had, if Joan ate 8 chips and the serving size is 50 chips and that is equal to 140 cal. and there are 8 servings per 50 chips how many cal. is 8
chips?
Answers
22.4 calories would be present in 8 chips.
To solve this problemThe provided information is useful.
According to the serving size, 50 chips have 140 calories.
50 chips provide 8 servings.
To calculate the number of calories in 8 chips, we can set up a proportion:
(50 chips) / (140 calories) = (8 chips) / (x calories)
Cross-multiplying, we get:
50 chips * x calories = 140 calories * 8 chips
50x = 1120
Dividing both sides by 50, we find:
x = 22.4 calories
Therefore, 22.4 calories would be present in 8 chips.
Learn more about proportion here : brainly.com/question/19994681
#SPJ1
given that f(x)=9x−8, what is the average value of f(x) over the interval [−5,6]? (enter your answer as an exact fraction if necessary.)
Answers
the average value of f(x) over the interval [−5,6] is 9/2.
To find the average value of f(x) over the interval [−5,6], we need to calculate the definite integral of f(x) from -5 to 6, and then divide the result by the length of the interval (which is 6 - (-5) = 11). So, we have:
(1/11) * ∫[-5,6] (9x - 8) dx
= (1/11) * [(9/2)x^2 - 8x]_[-5,6]
= (1/11) * [(9/2)*(6^2) - 8*6 - (9/2)*(-5^2) + 8*(-5)]
= (1/11) * [(9/2)*36 - 48 - (9/2)*25 - 40]
= (1/11) * [-81/2]
= -9/22
But we need to give our answer as an exact fraction, so we need to simplify. We can do this by multiplying the numerator and denominator by 2, which gives:
(2*(-9))/ (2*22) = -18/44 = -9/22
Therefore, the average value of f(x) over the interval [−5,6] is 9/2.
Conclusion: The average value of f(x) over the interval [−5,6] is 9/2, which we found by calculating the definite integral of f(x) over the interval and dividing the result by the length of the interval.
To learn more about fraction visit:
https://brainly.com/question/10354322
#SPJ11
Let P3 have the inner product given by evaluation at-2-1, 1, and 2. Let Po(t)-1. p1 (t)-2t, and p2 (t)-r a. Compute the orthogonal projection of p2 onto the subspace spanned by Po and p1 b. Find a polynomial q that is orthogonal to Po and P1, such that (Po P1.) is an orthogonal basis for Span(Po P1 P2). Scale the polynomial q so that its vector of values at (-2,-1,1,2) s(1,1,-1,1)
Answers
The polynomial q so that its Vector of values at (-2, -1, 1, 2) matches the vector s(1, 1, -1, 1), we can divide q by the norm of s
a) To compute the orthogonal projection of p2 onto the subspace spanned by Po and p1, we can use the orthogonal projection formula:
proj_v(u) = (u · v / ||v||^2) * v
where u is the vector to be projected (in this case, p2), and v is the vector spanning the subspace (in this case, Po and p1).
First, we need to find the vector v that spans the subspace. Since Po(t) = -1 and p1(t) = 2t, we can write v as a linear combination of Po and p1:
v = a * Po + b * p1
Substituting the values of Po and p1, we get:
v = a * (-1) + b * (2t) = -a + 2bt
Next, we calculate the inner product of p2 and v:
p2 · v = ∫[p2(t) * v(t)] dt
p2 · v = ∫[(r * (-1) * (-1) + r * (2t))] dt
= ∫[(r + 2rt)] dt
= r * t + rt^2
Now, we calculate the norm squared of v:
||v||^2 = ∫[(v(t))^2] dt
||v||^2 = ∫[(-a + 2bt)^2] dt
= ∫[(a^2 - 2abt + 4b^2t^2)] dt
= a^2t - abt^2 + (4/3)b^2t^3
Finally, we can compute the orthogonal projection of p2 onto the subspace:
proj_v(p2) = (p2 · v / ||v||^2) * v
proj_v(p2) = ((r * t + rt^2) / (a^2t - abt^2 + (4/3)b^2t^3)) * (-a + 2bt)
b) To find a polynomial q that is orthogonal to Po and p1, we can use the Gram-Schmidt process. We start with p2 as the initial vector and subtract its projection onto the subspace spanned by Po and p1:
q = p2 - proj_v(p2)
Since we have already calculated the projection in part a, we can substitute the values into the equation
q = p2 - ((r * t + rt^2) / (a^2t - abt^2 + (4/3)b^2t^3)) * (-a + 2bt)
Finally, to scale the polynomial q so that its vector of values at (-2, -1, 1, 2) matches the vector s(1, 1, -1, 1), we can divide q by the norm of s and evaluate it at those points:
q_scaled = q / ||s||
q_scaled(-2) = q(-2) / ||s||
q_scaled(-1) = q(-1) / ||s||
q_scaled(1) = q(1) / ||s||
q_scaled(2) = q(2) / ||s||
To know more about Vector .
https://brainly.com/question/12949818
#SPJ11
The orthogonal projection of p2 onto the subspace spanned by Po and p1 is the zero vector.
a) To find the orthogonal projection of p2 onto the subspace spanned by Po and p1, we first need to check if Po and p1 are orthogonal.
⟨Po, p1⟩ = Po(-2) p1(-2) + Po(-1) p1(-1) + Po(1) p1(1) + Po(2) p1(2)
= (1)(-4) + (0)(-2) + (1)(2) + (1)(4)
= 0
Since ⟨Po, p1⟩ = 0, Po and p1 are orthogonal. We can use the formula for orthogonal projection:
projPo,p1(p2) = (⟨p2, Po⟩ / ⟨Po, Po⟩) Po + (⟨p2, p1⟩ / ⟨p1, p1⟩) p1
First, we need to calculate the inner products:
⟨p2, Po⟩ = p2(-2) Po(-2) + p2(-1) Po(-1) + p2(1) Po(1) + p2(2) Po(2)
= r(1) + 2r(0) - r(1) - 2r(0)
= 0
⟨Po, Po⟩ = Po(-2) Po(-2) + Po(-1) Po(-1) + Po(1) Po(1) + Po(2) Po(2)
= 1 + 0 + 1 + 1
= 3
⟨p2, p1⟩ = p2(-2) p1(-2) + p2(-1) p1(-1) + p2(1) p1(1) + p2(2) p1(2)
= -2r(1) - r(0) + 2r(1) - r(0)
= 0
⟨p1, p1⟩ = p1(-2) p1(-2) + p1(-1) p1(-1) + p1(1) p1(1) + p1(2) p1(2)
= 4 + 0 + 4 + 4
= 12
Plugging in these values, we get:
projPo,p1(p2) = (0/3) Po + (0/12) p1
= 0
b) To find a polynomial q that is orthogonal to Po and p1 and forms an orthogonal basis with Po and p1, we can use the Gram-Schmidt process.
Let q0 = p2 = r, and let q1 = Po - projPo,p1(q0). We found projPo,p1(p2) to be 0 in part (a), so q1 = Po = 1.
Next, we orthogonalize q0 and q1:
q0' = q0 - projPo,p1(q0) = r
q1' = q1 - projPo,p1(q1) = Po = 1
Then, we normalize q1' by dividing by its norm:
q1'' = q1' / ||q1'|| = q1' / √⟨q1', q1'⟩
= q1' / √⟨Po, Po⟩
= (1/√3) q1'
= (1/√3) (1
Know more about orthogonal projection here:
https://brainly.com/question/2292926
#SPJ11
What is the quotient of the expression the quantity 28 times a to the fourth power times b plus 4 times a to the second power times b to the second power minus 12 times a times b end quantity divided by the quantity 4 a times b end quantity? 7a3 + ab + 3 7a3 + ab − 3 7a3 + 4ab + 8 7a3 + 4ab − 8
Answers
The quotient obtained when the expression 28a⁴b + 4a²b² - 12ab is divided by 4ab is 7a³ + ab - 3 (2nd option)
How do i determine the quotient?Quotient is the result obtained when we carry out division operation.
The quotient for the expression (28a⁴b + 4a²b² - 12ab) / 4ab can be obtain as illustrated below:
Expression: (28a⁴b + 4a²b² - 12ab) / 4abQuotient =?(28a⁴b + 4a²b² - 12ab) / 4ab
Factorizing the numerator, we have:
(28a⁴b + 4a²b² - 12ab) / 4ab = 4ab(7a³ + ab - 3) / 4ab
Canceling out 4ab, we have:
(28a⁴b + 4a²b² - 12ab) / 4ab = 7a³ + ab - 3
Thus, from the above calculation, we can conclude that the quotient for the expression (28a⁴b + 4a²b² - 12ab) / 4ab is 7a³ + ab - 3 (2nd option)
Learn more about quotient:
https://brainly.com/question/15302743
#SPJ1
given the velocity function v(t)=−t 8 m/sec for the motion of a particle, find the net displacement of the particle from t=4 to t=8. do not include any units in your answer.
Answers
Answer: To find the displacement of the particle from t = 4 to t = 8, we need to integrate the velocity function with respect to time over that interval:
∫[4, 8] v(t) dt = ∫[4, 8] (-t/8) dt
Using the power rule of integration, we get:
= [-t^2/16] evaluated at t=4 and t=8
= [-(8^2)/16 - (-4^2)/16]
= -16
Therefore, the net displacement of the particle from t = 4 to t = 8 is -16 units.
The net displacement of the particle from t=4 to t=8 is -15 m/s
To find the net displacement of a particle over a given time interval, we need to integrate its velocity function with respect to time over that interval. In this case, we are given the velocity function v(t) = -t/8.
∫[4,8] v(t) dt =
∫[4,8] (-t/8) dt =
[-t^2/16]_4^8
To find the net displacement from t=4 to t=8, we set up the definite integral:
∫[4,8] v(t) dt
Integrating the velocity function with respect to time, we have:
∫[4,8] (-t/8) dt
To evaluate the integral, we can apply the power rule of integration:
= [-t^2/16] from 4 to 8
Plugging in the upper and lower limits of integration, we have:
Therefore, the net displacement of the particle from t=4 to t=8 is -15 meters.
To know more about displacement refer here:
https://brainly.com/question/18125359
#SPJ11
i need the work shown for this question
Answers
Answer:
x = 16 , y = 116
Step-by-step explanation:
in an isosceles trapezoid
• any lower base angle is supplementary to any upper base angle
• the upper base angles are congruent
then
4x + 6x + 20 = 180
10x + 20 = 180 ( subtract 20 from both sides )
10x = 160 ( divide both sides by 10 )
x = 16
so
6x + 20 = 6(16) + 20 = 96 + 20 = 116
and
y = 116 ( upper base angles are congruent )
A polling company reported that 17% of 2286 surveyed adults said that they play baseball. Complete parts (a) through (d) below. a. What is the exact value that is 17% of 2286? The exact value is 0 (Type an integer or a decimal.) b. Could the result from part (a) be the actual number of adults who said that they play baseball? Why or why not? O A. No, the result from part (a) could not be the actual number of adults who said that they play baseball because a count of people must result in a whole number. OB. Yes, the result from part (a) could be the actual number of adults who said that they play baseball because the results are statistically significant. OC. Yes, the result from part (a) could be the actual number of adults who said that they play baseball because the polling numbers are accurate. OD. No, the result from part (a) could not be the actual number of adults who said that they play baseball because that is a very rare activity. c. What could be the actual number of adults who said that they play baseball? The actual number of adults who play baseball could be (Type an integer or a decimal.) d. Among the 2286 respondents, 297 said that they only play hockey. What percentage of respondents said that they only play hockey? (Round to two decimal places as needed.)
Answers
Answer:
Step-by-step explanation:
a. The exact value that is 17% of 2286 is 0 (zero).
b. O A. No, the result from part (a) could not be the actual number of adults who said that they play baseball because a count of people must result in a whole number.
c. The actual number of adults who said that they play baseball could be any value between 0 and 2286. Without further information, we cannot determine the exact number.
d. To calculate the percentage of respondents who said they only play hockey, we divide the number of respondents who only play hockey (297) by the total number of respondents (2286), and then multiply by 100:
Percentage = (297 / 2286) * 100
Percentage ≈ 12.99%
Approximately 12.99% of respondents said that they only play hockey.
a pot containing 410 g of water is placed on the stove and is slowly heated from 25°c to 92°c. Calculate the change of entropy of the water in J/K
Answers
The change in entropy (ΔS) of the water can be calculated using the formula:
ΔS = mcΔT / T
where m is the mass of the water (410 g), c is the specific heat capacity of water (4.18 J/gK), ΔT is the change in temperature (92°C - 25°C), and T is the final temperature in Kelvin (92°C + 273.15).
1. Convert the final temperature to Kelvin: 92°C + 273.15 = 365.15 K
2. Calculate the change in temperature: ΔT = 92°C - 25°C = 67°C
3. Use the formula to calculate the change in entropy:
ΔS = (410 g)(4.18 J/gK)(67°C) / 365.15 K
By calculating the values, the change in entropy (ΔS) of the water is approximately 98.42 J/K.
To learn more about entropy visit:
https://brainly.com/question/13135498
#SPJ11
find a function g(x) so that y = g(x) is uniformly distributed on 0 1
Answers
To find a function g(x) that results in a uniformly distributed y = g(x) on the interval [0,1], we can use the inverse transformation method. This involves using the inverse of the cumulative distribution function (CDF) of the uniform distribution.
The CDF of the uniform distribution on [0,1] is simply F(y) = y for 0 ≤ y ≤ 1. Therefore, the inverse CDF is F^(-1)(u) = u for 0 ≤ u ≤ 1.
Now, let's define our function g(x) as g(x) = F^(-1)(x) = x. This means that y = g(x) = x, and since x is uniformly distributed on [0,1], then y is also uniformly distributed on [0,1].
In summary, the function g(x) = x results in a uniformly distributed y = g(x) on the interval [0,1].
Hello! I understand that you want a function g(x) that results in a uniformly distributed variable y between 0 and 1. A simple function that satisfies this condition is g(x) = x, where x is a uniformly distributed variable on the interval [0, 1]. When g(x) = x, the variable y also becomes uniformly distributed over the same interval [0, 1].
To clarify, a uniformly distributed variable means that the probability of any value within the specified interval is equal. In this case, for the interval [0, 1], any value of y will have the same likelihood of occurring. By using the function g(x) = x,
To know more about Functions visit :
https://brainly.com/question/12431044
#SPJ11
devise a synthesis of the epoxide b from alcohol a.
Answers
The synthesis of epoxide B from alcohol A involves four main steps: protection of the hydroxyl group, oxidation of the alcohol to an aldehyde, epoxidation of the aldehyde to form the epoxide, and finally, removal of the protecting group to yield the desired epoxide B.
To synthesize epoxide B from alcohol A, several steps need to be taken. Here is a long answer detailing the process:
Step 1: Protect the hydroxyl group
The first step in synthesizing epoxide B from alcohol A is to protect the hydroxyl group. This is necessary to prevent it from reacting with the epoxide during the subsequent steps.
One common protecting group for alcohol is the silyl ether group.
To do this, alcohol A is treated with a silylating agent such as trimethylsilyl chloride (TMSCl) in the presence of a base such as triethylamine.
This results in the formation of the silyl ether derivative of alcohol A.
Step 2: Oxidize the alcohol to an aldehyde
The next step is to oxidize the alcohol to an aldehyde. This can be achieved using an oxidizing agent such as pyridinium chlorochromate (PCC). The aldehyde product is then purified by distillation or column chromatography.
Step 3: Epoxidation
The aldehyde is then epoxidized using a peracid such as m-chloroperbenzoic acid (MCPBA). This results in the formation of the desired epoxide B.
The epoxide is then purified by distillation or column chromatography.
Step 4: Deprotection
The final step is to remove the silyl ether-protecting group from the epoxide.
This can be achieved using an acid such as trifluoroacetic acid (TFA). After the removal of the protecting group, epoxide B is obtained as the final product.
In summary, the synthesis of epoxide B from alcohol A involves four main steps: protection of the hydroxyl group, oxidation of the alcohol to an aldehyde, epoxidation of the aldehyde to form the epoxide, and finally, removal of the protecting group to yield the desired epoxide B.
Know more about oxidation here:
https://brainly.com/question/25886015
#SPJ11
A green pea pod plant, that had a yellow pea pod parent, is crossed with a yellow pea pod plant. (Remember green is dominant to yellow. ) What percentage of the offspring will have green pea pods?
Answers
In this cross, where a green pea pod plant with a yellow pea pod parent is crossed with a yellow pea pod plant, approximately 50% of the offspring will have green pea pods.
In this scenario, green is the dominant trait and yellow is the recessive trait. The green pea pod plant that had a yellow pea pod parent is heterozygous for the trait, meaning it carries one dominant green allele and one recessive yellow allele. The yellow pea pod plant, on the other hand, is homozygous recessive, carrying two recessive yellow alleles.
When these two plants are crossed, their offspring will inherit one allele from each parent. There are two possible combinations: the offspring can inherit a green allele from the green pea pod plant and a yellow allele from the yellow pea pod plant, or they can inherit a green allele from the green pea pod plant and another green allele from the yellow pea pod plant.
Therefore, approximately 50% of the offspring will inherit the green allele and have green pea pods, while the other 50% will inherit the yellow allele and have yellow pea pods. This is because the green allele is dominant and masks the expression of the recessive yellow allele.
Learn more about approximately here:
https://brainly.com/question/31695967
#SPJ11
young's modulus of nylon is 3.7 x 10^9 N/M^2. A force of 6.0 x 10^5N is applied to a 1.5-m lenght of nylon of cross sectional area 0.25 m^2.
(a) find the stress in the nylon.
(b) by what amount does the nylon stretch?
Answers
The answer to force being applied to Young's modulus of nylon is - The stress in the nylon is 1.6 x 10^8 N/m^2, and the amount by which the nylon stretches is 0.0649 m.
Let's start with part (a) of the question:
(a) To find the stress in the nylon, we can use the formula:
Stress = Force / Area
We are given the force as 6.0 x 10^5 N and the area as 0.25 m^2. So, plugging those values into the formula, we get:
Stress = 6.0 x 10^5 N / 0.25 m^2
Stress = 2.4 x 10^6 N/m^2
Therefore, the stress in the nylon is 2.4 x 10^6 N/m^2.
(b) Now, to find the amount by which the nylon stretches, we can use the formula:
Stress = Young's Modulus x Strain
We know the Young's Modulus of nylon as 3.7 x 10^9 N/m^2, and we need to find the strain. We can use the formula:
Strain = Extension / Original Length
We are given the original length of the nylon as 1.5 m. To find the extension, we need to use the formula:
Extension = Force / (Young's Modulus x Area)
Plugging in the values, we get:
Extension = 6.0 x 10^5 N / (3.7 x 10^9 N/m^2 x 0.25 m^2)
Extension = 0.0649 m
Therefore, the extension of the nylon is 0.0649 m. Now, we can find the strain as:
Strain = Extension / Original Length
Strain = 0.0649 m / 1.5 m
Strain = 0.04327
Finally, plugging the values into the formula for stress, we get:
Stress = Young's Modulus x Strain
Stress = 3.7 x 10^9 N/m^2 x 0.04327
Stress = 1.6 x 10^8 N/m^2
Therefore, the stress in the nylon is 1.6 x 10^8 N/m^2, and the amount by which the nylon stretches is 0.0649 m.
To know more about Young's modulus refer here :
https://brainly.com/question/30756002#
#SPJ11
I’m going back home now
Answers
Answer:
write a letter about you receiveing a gift from aunt
Lucy's Rental Car charges an initial fee of $30 plus an additional $20 per day to rent a car. Adam's Rental Car
charges an initial fee of $28 plus an additional $36 per day. For what number of days is the total cost charged
by the companies the same?
Answers
The number of days for which the companies charge the same cost is given as follows:
0.125 days.
How to define a linear function?The slope-intercept equation for a linear function is presented as follows:
y = mx + b
In which:
m is the slope.b is the intercept.For each function in this problem, the slope and the intercept are given as follows:
Slope is the daily cost.Intercept is the fixed cost.Hence the functions are given as follows:
L(x) = 30 + 20x.A(x) = 28 + 36x.Then the cost is the same when:
A(x) = L(x)
28 + 36x = 30 + 20x
16x = 2
x = 0.125 days.
More can be learned about linear functions at https://brainly.com/question/15602982
#SPJ4
Why does the
characters in this story all seem to have common nouns as names (blade, storm, chapel)?
Answers
The reason why the characters in the story all seem to have common nouns as names (blade, storm, chapel) is to indicate that the story is a fable.
A fable is a brief story that teaches a moral or lesson through the use of animals, mythical creatures, and inanimate objects. The author of the fable usually tries to teach the readers a lesson in an entertaining way that captures their attention.
The use of common nouns as names in a fable is a common literary technique that is used to teach lessons through storytelling.
The author uses common nouns as names to emphasize the moral or lesson that he/she wants to teach.In this case, the common nouns used as names (blade, storm, chapel) are used to highlight the character's personalities and to emphasize the moral or lesson that the author wants to teach.
To know more about fable visit:
https://brainly.com/question/14299030
#SPJ11
A small computer store has room to display up to three computers for sale. Customers come at times of a Poisson process with rate 2 per week to buy a computer and will buy one if at least 1 is available. When the store bas only one computer left, it plaes an order for two more computets. Because the store always goes for the cheapest shipping option, they get the world's worst service, so the order takes exponentially distributed amount of time with mean 1 neek to arrive. Naturally, while waiting for a shipment, sometimes their inventory levels are reduced to 0 (a) Find the transition rate matrix Q (b) Find the stationary distribution for the inventory levels. (e) At what rate does the store make sales? (Hint: you need the answer to (b) for this)
Answers
The rate of sales is 2*(32/39)=64/39 per week.
To find the transition rate matrix Q, we need to consider the different possible inventory levels and the rates of transition between them. Let's label the states as 0, 1, 2, and 3, representing the number of computers in stock.
If there are 0 or 1 computers in stock, the arrival rate is 2 per week and the transition rate to the next state is 2. If there are 2 computers in stock, the arrival rate is still 2 per week, but the transition rate to the next state is 4 (since there are two opportunities for a customer to buy).
Finally, if there are 3 computers in stock, the arrival rate is 0 (since customers only buy when at least one computer is available), and the transition rate to the next state is 0 if there is no pending order, or 1/2 if there is.
The resulting transition rate matrix Q is:
[ -2 2 0 0 ]
[ 2 -4 2 0 ]
[ 0 2 -4 1/2 ]
[ 0 0 1/2 0 ]
To find the stationary distribution for the inventory levels, we need to solve for the vector πQ=0, where π is the stationary distribution and Q is the transition rate matrix. Solving this system of equations, we get:
π0 = 16/39, π1 = 20/39, π2 = 4/13, π3 = 0
This means that the store is most likely to have 1 computer in stock, followed by 0, 2, and never 3.
To find the rate of sales, we need to consider the total arrival rate of customers, which is 2 per week. However, customers will only buy when at least 1 computer is available, which occurs with probability π1+π2+π3=20/39+4/13+0=32/39.
To learn more about : sales
https://brainly.com/question/24951536
#SPJ11
(a) The transition rate matrix Q =
[ -2 2 0 0 ]
[ 0 -1 0 1 ]
[ 0 0 -1 1 ]
[ 0 2 0 -2 ]
(b) The store will have 1 computer in stock about 14% of the time, 2 computers in stock about 29% of the time, and 3 computers in stock about 57% of the time.
(c) The store makes sales at a rate of 1 per week on average.
To find the transition rate matrix Q, we need to consider all the possible states of the system. In this case, the inventory level can be 0, 1, 2, or 3. Let's represent these states by 0, 1, 2, and 3, respectively. The transition rate from state i to state j is denoted by qij.
Starting with state 0, customers arrive at a rate of 2 per week and buy a computer if one is available. Therefore, the transition rate from 0 to 1 is q01 = 2. Since the store orders 2 more computers when it has only 1 left, the transition rate from 1 to 3 is q13 = 1/1 = 1 (because the order takes 1 week on average to arrive). Similarly, the transition rate from 2 to 3 is q23 = 1/1 = 1. Once the order arrives, the inventory level goes up by 2, so the transition rate from 3 to 1 is q31 = 2. Finally, the transition rates for staying in the same state are q00 = 0, q11 = 0, q22 = 0, and q33 = 0.
Putting all these transition rates in a matrix, we get
Q =
[ -2 2 0 0 ]
[ 0 -1 0 1 ]
[ 0 0 -1 1 ]
[ 0 2 0 -2 ]
To find the stationary distribution for the inventory levels, we need to solve the equation Qπ = 0, where π is the vector of stationary probabilities. Since the sum of probabilities in any state must be 1, we also have the condition π0 + π1 + π2 + π3 = 1.
Solving the system of equations, we get
π = [ 1/7 2/7 2/7 2/7 ]
This means that the store will have 1 computer in stock about 14% of the time, 2 computers in stock about 29% of the time, and 3 computers in stock about 57% of the time.
Finally, to find the rate at which the store makes sales, we need to consider the transitions from states 1, 2, and 3 (since no sales can happen in state 0). The total rate of leaving these states is λ = q13π3 + q23π3 + q31π1 = 1/7 + 2/7 + 4/7 = 1. Therefore, the store makes sales at a rate of 1 per week on average.
Visit here to learn more about transition rate matrix:
brainly.com/question/31473469
#SPJ11
A company makes 140 bags. 28 of the bags have buttons but no zips. 47 of the bags have zips but no buttons. 27 of the bags have neither zips nor buttons. A bag is selected at random. What is the probability that the bag has buttons?
Answers
The probability that the bag selected at random has buttons is 1/5 or 0.2.
To find the probability that the bag has buttons, we need to consider the number of bags that have buttons and the total number of bags.
Given information:
Total number of bags = 140
Number of bags with buttons = 28
To calculate the probability, we divide the number of bags with buttons by the total number of bags:
Probability = Number of bags with buttons / Total number of bags
Probability = 28 / 140
Simplifying the fraction, we get:
Probability = 1 / 5
Therefore, the probability that the bag selected at random has buttons is 1/5 or 0.2.
Learn more about probability here:
brainly.com/question/11234923
#SPJ1
use the given transformation to evaluate the integral. r 8x2 da, where r is the region bounded by the ellipse 25x2 4y2 = 100; x = 2u, y = 5v
Answers
Using the given transformation, r = {(x,y) | 25x^2/4 + y^2/4 = 1} maps to R = {(u,v) | u^2 + v^2 = 1}, and we have:
∬r 8x^2 da = 80∬R u^2 (2 du)(5 dv) = 800∫0^1 u^2 du ∫0^1 dv = 800/3
Therefore, ∬r 8x^2 da = 800/3.
We are given the region r bounded by the ellipse 25x^2/4 + y^2/4 = 1 and the transformation x = 2u, y = 5v. We want to evaluate the integral ∬r 8x^2 da over the region r.
To use the given transformation, we need to find the image R of the region r under the transformation. Substituting x = 2u and y = 5v into the equation of the ellipse, we get:
25(2u)^2/4 + (5v)^2/4 = 1
25u^2 + v^2 = 1
This is the equation of a circle with radius 1 centered at the origin. Therefore, the image R of r under the transformation is the unit circle centered at the origin.
To evaluate the integral using the transformed variables, we use the fact that da = |J| du dv, where J is the Jacobian matrix of the transformation. In this case, we have:
J = |[∂x/∂u ∂x/∂v]|
|[∂y/∂u ∂y/∂v]|
Substituting x = 2u and y = 5v, we have:
J = |[2 0]|
|[0 5]|
So, |J| = 10. Therefore, we have:
∬r 8x^2 da = ∬R 8(2u)^2 |J| du dv
= 80∫0^1 ∫0^1 u^2 du dv
Evaluating the integral gives:
∬r 8x^2 da = 800/3.
Learn more about integral :
https://brainly.com/question/18125359
#SPJ11
let f(x,y) = exy sin(y) for all (x,y) in r2. verify that the conclusion of clairaut’s theorem holds for f at the point (0,π/2).
Answers
To verify that the conclusion of Clairaut's theorem holds for f at the point (0,π/2), we need to check that the partial derivatives of f with respect to x and y are continuous at (0,π/2) and that they are equal at this point. Since e^(π/2) is not equal to π/2, the conclusion of Clairaut's theorem does not hold for f at the point (0,π/2).
First, let's find the partial derivative of f with respect to x:
∂f/∂x = yexy sin(y)
Now, let's find the partial derivative of f with respect to y:
∂f/∂y = exy cos(y) + exy sin(y)
At the point (0,π/2), we have:
∂f/∂x = π/2
∂f/∂y = e^(π/2)
Both partial derivatives exist and are continuous at (0,π/2).
To check that they are equal at this point, we can simply plug in the values:
∂f/∂y evaluated at (0,π/2) = e^(π/2)
∂f/∂x evaluated at (0,π/2) = π/2
Since e^(π/2) is not equal to π/2, the conclusion of Clairaut's theorem does not hold for f at the point (0,π/2).
To know more about Clairaut's theorem visit:
https://brainly.com/question/13513921
#SPJ11
The general form of the solutions of the recurrnce relation with the following characteristic equation is: (r+ 5)(r-3)^2 = 0 A. an = (ɑ1 - ɑ2n) (3)^n + ɑ3(-5)^n
B. an = (ɑ1 + ɑ2n) (3)^n + ɑ3(5)^n
C. an = (ɑ1 + ɑ2n) (3)^n + ɑ3(-5)^n
D. None of the above
Answers
"The correct option is C".where $\alpha_1$, $\alpha_2$, $\alpha_3$ are constants determined by the initial conditions of the recurrence relation, and $k$ is either $0$ or $1$.
The characteristic equation of a linear homogeneous recurrence relation is obtained by assuming the solution has the form of a geometric progression, i.e., $a_n = r^n$. Therefore, the characteristic equation corresponding to the recurrence relation given is $(r+5)(r-3)^2=0$. This equation has three roots: $r=-5$ and $r=3$ (with multiplicity 2).
According to the theory of linear homogeneous recurrence relations, the general solution can be written as a linear combination of terms of the form $n^kr^n$, where $k$ is a nonnegative integer and $r$ is a root of the characteristic equation. Since there are two roots, the general solution will have two terms.
For the root $r=-5$, the corresponding term is $\alpha_1 (-5)^n$. For the root $r=3$, the corresponding terms are $\alpha_2 n^k(3)^n$ and $\alpha_3(3)^n$, where $k$ is either $0$ or $1$ (since the root $r=3$ has multiplicity $2$).
The general form of the solutions of the recurrence relation is:
an=α1(−5)n+α2nk(3)n+α3(3)n,an=α1(−5)n+α2nk(3)n+α3(3)n.
For such more questions on Recurrence relation:
https://brainly.com/question/4082048
#SPJ11
The general form of the solutions of the recurrence relation with the following characteristic equation is: (r+ 5)(r-3)^2 = 0
is A. an = (ɑ1 - ɑ2n) (3)^n + ɑ3(-5)^n
The general form of the solutions for the given recurrence relation with the characteristic equation (r+5)(r-3)^2 = 0 can be found by examining its roots. The roots are r = -5, 3, and 3 (the latter having multiplicity 2).
For this type of problem, the general solution is expressed as:
an = ɑ1(c1)^n + ɑ2(c2)^n + ɑ3(n)(c3)^n
Here, c1, c2, and c3 represent the distinct roots of the characteristic equation. Since we have roots -5 and 3 (with multiplicity 2), the general solution will be:
an = ɑ1(-5)^n + ɑ2(3)^n + ɑ3(n)(3)^n
Comparing this with the given options, the correct answer is:
A. an = (ɑ1 - ɑ2n) (3)^n + ɑ3(-5)^n
Visit here to learn more about recurrence relation:
brainly.com/question/31384990?
#SPJ11