Answers
Answer: [tex]\sqrt{407}[/tex]
Step-by-step explanation:
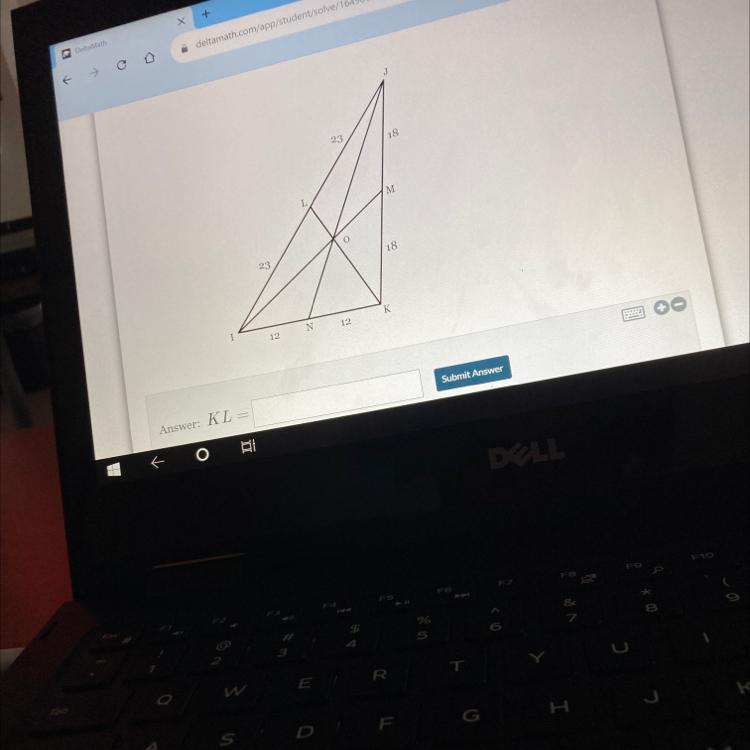
In this triangle, we know that [tex]IJ=46, IK=24, JK=36[/tex].
So, using the Law of Cosines in triangle IJK,
[tex]36^2 = 46^2 + 24^2 - 2(46)(24) \cos (\angle JIK)\\\\-1396=-2(46)(24) \cos(\angle JIK)\\\\\cos (\angle JIK)=\frac{349}{552}[/tex]
Using the Law of Cosines in the triangle LIK,
[tex](KL)^2 = 23^2 + 24^2 - 2(23)(24) \cos (\angle JIK)\\\\(KL)^2 = 23^2 + 24^2 - 2(23)(24)\left(\frac{349}{552} \right)\\\\(KL)^2 = 407\\\\KL=\sqrt{407}[/tex]
Related Questions
60% of the books in a library are for adults, 5% are for young people and the rest are for children. If there are 280 books for children, how many books are there altogether?
Answers
Answer:
800 books
problem solving steps:
adults:60%
young people:5%
children=100%-60%-5%
=35%
35%=280 books
1%=280÷35
=8
100%=800
so,there are 800 books
How is the graph of y(x-1)²-3 transformed to produce the graph of y(x+4)²
O The graph is translated left 5 units, compressed vertically by a factor of 2, and translated up 3 units.
O The graph is stretched vertically by a factor of 2, translated left 5 units, and translated up 3 units.
The graph is translated left 5 units, compressed horizontally by a factor of 2, and translated down 3 units.
O The graph is stretched horizontally by a factor of 2, translated left 5 units, and translated down 3 units.
Mark this and return
Save and Exit
Next
Submit
Answers
The transformations are:
Shift up 3 units.
Shift left 5 units.
Vertical compression of scale factor 2.
The correct option is the first one.
Here, we have,
Here we start with the original function:
y = (x - 1)^2 - 3
And it will be transformed into the new function:
y = (1/2)*(x + 4)^2
So let's start with the first function, and apply transformations until we reach the new one.
y = (x - 1)^2 - 3
If we shift it up by 3 units, then we get:
y = [ (x - 1)^2 - 3 ] + 3 = (x - 1)^2
If now we shift it to the left 5 units, then we get:
y = ( (x + 5) - 1)^2 = (x + 4)^2
finally, we compress the graph by a factor of 2, so we get:
y = (1/2)*(x + 4)^2
The order may be different, but from that we conclude that the correct option is the first option.
If you want to learn more about transformations:
brainly.com/question/4289712
#SPJ1
complete question:
graph of y = (x- 1)2 -3 transformed to produce the graph of y = - 1/2(X+-4)2?
O The graph is translated left 5 units, compressed vertically by a factor a of 2, and translated up 3 units.
The graph is stretched vertically by a factor of 2, translated left 5 units, and translated up 3 units.
• The graph is translated left 5 units, compressed horizontally by a factor of 2, and translated down 3 units.
• The graph is stretched horizontally by a factor of 7, translated left 5 units, and translated down 3 units:
Which equation can be used to solve for � xx in the following diagram?
Answers
Equation which can be used to solve for the value of x is
3x° + 2x° + 80 °= 180° .
Straight angle pair is the sum of two or more angles that are in pair of angles that form a straight line is always equal to 180°.
As shown in the diagram angle on the lines are -
3x ° , 80° , 2x° respectively
Sum of all these angle will be equal to 180°.
3x° + 2x° + 80° = 180
The correct equation to find the value of x is 3x° + 2x° + 80° = 180° .
To know more about equation click here :
https://brainly.com/question/31086219
#SPJ1
What are the solutions to the system of equations graphed?
Answers
Answer:
(- 2, 0 ) , (1, - 3 )
Step-by-step explanation:
the solutions to the system of equations are at the points of intersection with the curve and the straight line.
points of intersection are at (- 2, 0 ) and (1, - 3 ) , then
solutions are (- 2, 0 ) , (1, - 3 )
Please help I’ll mark you as brainliest if correct!
Answers
Using similar side theorem, the side with equivalent proportion to the given side is RQ/SQ
What is similar side theorem?Similar triangles are triangles that have the same shape, but their sizes may vary. All equilateral triangles, squares of any side lengths are examples of similar objects. In other words, if two triangles are similar, then their corresponding angles are congruent and corresponding sides are in equal proportion.
In this problem, we can use this same theory to find the equivalent side of the given proportion.
OQ / PQ = RQ / SQ
The equivalent side is RQ/SQ
Learn more on similar side theorem here;
https://brainly.com/question/12960403
#SPJ1
What is the scale of the x-axis in this coordinate graph?
A. 1 tick mark represents 0.1 unit
B. 1 tick mark represents 0.2 unit
C. 1 tick mark represents 0.3 unit
D. 1 tick mark represents 0.4 unit
Answers
Answer:
B. 1 tick mark represents 0.2 unit
Step-by-step explanation:
Looking at the axis and going over 2 tick marks is .4
.4 /2 = .2
Each tick mark is .2 units
Can someone help me find the surface area of these cylinders??
Answers
The surface area for each of the cylinders is given as follows:
13. 126 yd².
14. 490 m².
15. 283 mm².
16. 297 cm².
How to obtain the surface area of a cylinder?The surface area of a cylinder of radius r and height h is given by the equation presented as follows, which combines the base area with the lateral area:
S = 2πrh + 2πr²
S = 2πr(h + r)
Item 13:
r = 2 yd and h = 8 yd, hence the surface area is given as follows:
S = 2π x 2(2 + 8)
S = 126 yd².
Item 14:
r = 6 m and h = 7 m, hence the surface area is given as follows:
S = 2π x 6(6 + 7)
S = 490 m².
Item 15:
r = 3 mm and h = 12 mm, hence the surface area is given as follows:
S = 2π x 3(3 + 12)
S = 283 mm².
Item 16:
r = 3.5 mm and h = 10 mm, hence the surface area is given as follows:
S = 2π x 3.5(3.5 + 10)
S = 297 cm².
More can be learned about cylinder at brainly.com/question/9554871
#SPJ1
-8.915444681 round to nearest hundred miles
Answers
On rounding the given number to nearest hundred miles will give the result -8.92.
Rounding to nearest hundred miles refers to changing the number present on hundreds place. We see that the number 8 is at unit's place, 9 is at tenth's place and 2 is at hundred's place.
Based on the rules of rounding, we will check the number to the right of number on hundred's place. Since the next number is 5, the number we will round the number 1 present at hundred's place. Hence, the final number will be -8.92.
Learn more about rounding -
https://brainly.com/question/22511490
#SPJ1
Write the equation of the circle for which ý(22, 21) and p(6, 23) are the endpoints of
a diameter of the circle.
Answers
Answer:
[tex](x-14)^2 +(y-22)^2 = (\sqrt{65})^2[/tex]
Step-by-step explanation:
If the two given points are the extremes of the diameter, the center of the circle has to be its middle point - that we can find by taking the average of the coordinates. The center thus sits in
[tex](\frac{22+6}2; \frac{21+23}2)[/tex] or [tex](14; 22)[/tex]. At this point we either find the length of the diameter and halve it, or the distance between the center and either point. Let's go for the diameter.
[tex]r=\sqrt{(22-6)^2+(21-23)^2}=\sqrt{16^2+2^2} = \sqrt {260}=2\sqrt{65}[/tex]. That makes our radius half of that. We can easily write the equation of the circle now:
[tex](x-14)^2 +(y-22)^2 = (\sqrt{65})^2[/tex]
Now, in theory you can improve it by multiplying it out and taking every term to the LHS, but I think it's good enough like that.
Three students share pawpaw as follows: Mark get 1/4 of the total and the remainder is shared between Eric and Francis in a ratio 2:3. If Eric get 48 pawpaws does Mark and Francis had ?
Answers
The total number of pawpaws was 160, which can be found by using simple equations considering the amount taken by Eric and the proportion.
How to find the total numberLet's start by finding out how many pawpaws are left after Mark takes 1/4 of the total. Let T be the total number of pawpaws. Mark gets 1/4 of T, which means there are 3/4 of T left:
3/4T = Total number of pawpaws - Mark's share
3/4T = T - 1/4T
3/4T = 3/4T
So, 3/4T is the amount shared between Eric and Francis. The ratio of Eric's share to Francis' share is 2:3. Let's call Eric's share E and Francis's share F.
E/F = 2/3
We can use this ratio to write an equation for Eric's share in terms of F:
E/F = 2/3
E = (2/3)F
We know Eric's share is 48, so we can substitute that into the equation and solve for F:
E = (2/3)F
48 = (2/3)F
F = (48*3)/2
F = 72
So, Francis has 72 pawpaws.
We can now find out how many pawpaws Mark got:
Mark's share + Eric's share + Francis's share = Total number of pawpaws
1/4T + E + F = T
1/4T + 48 + 72 = T
T = 480/3
T = 160
So, the total number of pawpaws is 160. Mark got 1/4 of the total, which is:
Mark's share = (1/4)*160 = 40
Learn more about equations here:
https://brainly.com/question/2972832
#SPJ1
PLS HELP ME OUT MARKING AS BRAINlist
Answers
Answer:
The answer is 176
Step-by-step explanation:
First lets find the area of rectangle by multiplying 16 by 8 to get 128.
Now lets find the area of each triangle. We know that one side is 6 cm and the base of both is 16.
So to find the base of one triangle we divide 16 by 2 to get 8.
Now we know that the base of one triangle is 8, so lets sub. that into the equation for a triangle. 1/2(b)(h) to get
1/2(6)(8)=24
Since there are two triangle 24+24=48 for area of both triangles
Now lets add that to the answer for the rectangle to get area for whole structure
128+48 = 176
So the answer is 176
HOPE THAT HELPS :)
Which of the following can be used to evaluate the series 8∑k=1 5(2/3)^k-1?
Answers
The evaluation of the geometric series is found as:
[tex]5(1- \frac{2}{3}^{8} / 1- \frac{2}{3} )[/tex]
How do we evaluate any given series?The given series is
[tex]8∑k=1 5(2/3)^k-1[/tex]
A geometric series is described as the sum of an infinite number of terms that have a constant ratio between successive terms.
Since this is a geometric series, we apply formula for the sum of the first k terms.
[tex]S= a( 1- r^{k} / 1-r )[/tex]
From the series, first term a = 5, common ratio r = 2/3 , k = 8
We substitute the values to obtain:
he evaluation of the series is found as:
[tex]5(1- \frac{2}{3}^{8} / 1- \frac{2}{3} )[/tex]
Geometric series finds its applications in Physics, engineering, biology, economics, computer science, queueing theory, and finance.
Learn more about geometric series at:
https://brainly.com/question/24643676
#SPJ1
complete question is attached in image
Diondra wants to know the most popular movie of this year but is unsure of the best way to determine this answer. Which of the following questions would Diondra ask that does NOT allow for variability?
Which movie did her best friend like the most?
How many awards did each movie win?
What is the total dollar amount that each movie made from ticket sales?
How many weeks did each movie play in the theater?
Answers
The question that Diondra would ask that does not allow for variability is A. Which movie did her best friend like the most?
How does this question not show variability ?The other three questions ("How many awards did each movie win?", "What is the total dollar amount that each movie made from ticket sales?", and "How many weeks did each movie play in the theater?") all offer metrics by which a movie's popularity could be measured, and those measurements could vary from movie to movie.
However, the question about her best friend's favorite movie depends solely on the opinion of one individual, not a variable measure, and therefore doesn't allow for variability.
Find out more on variability at https://brainly.com/question/12872866
#SPJ1
Joe King thinks he is "top notch" and buys a bouquet of flowers to pass out to all the ladies... The bouquet has 7 purple tulips, 9 yellow daisies and 12 pink roses. He grabs a flower from the bouquet and gives it to Anita Bath. Then Joe grabs another flower and gives it to Lois Price.
What is the probability that Anita gets a purple tulip and Lois gets a pink rose?
Answers
The probability that Anita gets a purple tulip and Lois gets a pink rose is 1/9.
How to calculate the probabilityTotal number of flowers in the bouquet = 7 purple tulips + 9 yellow daisies + 12 pink roses = 28 flowers.
P(Anita gets a purple tulip) = 7 purple tulips / 28 total flowers = 7/28 = 1/4.
P(Lois gets a pink rose) = 12 pink roses / 27 remaining flowers = 12/27 = 4/9.
P(Anita gets a purple tulip and Lois gets a pink rose) = P(Anita gets a purple tulip) * P(Lois gets a pink rose)
= (1/4) * (4/9) = 1/9.
Therefore, the probability that Anita gets a purple tulip and Lois gets a pink rose is 1/9.
Learn more about probability at https://brainly.com/question/13604758
#SPJ1
A chambered nautilus is a marine animal that lives in the outermost chamber of its shell
Answers
The chambered nautilus is a fascinating marine animal that belongs to the family of cephalopods.
It is notable for its unique, spiral-shaped shell that is divided into a series of chambers.
The nautilus lives in the outermost chamber of its shell, which it can control by adjusting the amount of gas and fluid inside it. This allows the nautilus to regulate its buoyancy and move up or down in the water column.
The nautilus has been around for millions of years and is sometimes called a "living fossil" because of its ancient lineage.
Unfortunately, due to overfishing and habitat destruction, many species of nautilus are now endangered.
To Know more about Marine animals here
https://brainly.com/question/3583133
#SPJ1
The given question is incomplete, the complete question is:
A chambered nautilus is a marine animal form which family?
johnny can build in 3 1/2 lego planes in 60 minutes. how many can he build in 40 minutes?
Answers
The number of lego planes that can be build in 40 minutes is A = 2.33
Given data ,
Johnny can build in 3 1/2 lego planes in 60 minutes
On dividing the number of planes he can build in 60 minutes (3 1/2) by 60:
From the proportion , we get
To find out how many planes he can build in 40 minutes, we can multiply the amount he can build in one minute by 40:
3.5 / 60 = A / 40
Multiply by 40 on both sides , we get
A = 2.33
Hence , Johnny can build approximately 2.33 lego planes in 40 minutes
To learn more about proportion click :
https://brainly.com/question/7096655
#SPJ1
jasmine bikes the same distance every day. in 8 days, she biked a total of 32 miles. How far will she bike in 5 days?
Answers
Answer:
20
Step-by-step explanation:
She biked an equal amount each day for 8 days to a total of 32 miles. We can write that as 8x = 32. 32/8 = 4 so x = 4. To find how much shell bike in 5 days, we multiply it by x(4). 5*4 = 20.
Can someone help me with this? Thank you
Answers
The area of the triangle is 6 sq units.
What is the area of the triangle?The area of the triangle is calculated by applying the following formula;
A = ¹/₂ x b x h
where;
b is the base of the triangleh is the height of the triangleThe base of the triangle = 3 - 0 = 3
The vertical height of the triangle = 5 - 1 = 4
Area = ¹/₂ x 4 x 3
Area = 6 sq units.
Thus, the area of the triangle is a function of base and height.
Learn more about area of triangles here: https://brainly.com/question/21735282
#SPJ1
The circle graph shows how Josh's family budgets a total of $6200 for the month.
Housing
$1178
Category
Clothing
Insurance
Transportation
Taxes
$1364
Taxes
Food
$868
$248 Insurance
$186
Utilities
$496
Savings
$434
Find the percentage of the total budgeted for each category listed below.
Percentage
0%
0%
0%
Clothing
Entertainment
$682
Answers
The percentage of the total budgeted category is given by
a) Clothing : 12 %
b) Insurance : 3 %
c) Taxes : 22 %
Given data ,
Let the percentage value be represented as A
Now , the value of A is
Let the total budgeted amount be = $ 6,200
Now , the amount for clothing = $ 744
So , the percentage for clothing = 744 / 6200 = 12 %
And , the amount for insurance = $ 186
Now , the percentage for insurance = 186 / 6200 = 3 %
And , the amount for taxes = $ 1,364
So , the percentage for taxes = 1364 / 6200 = 22 %
Hence , the percentages are solved
To learn more about percentage click :
https://brainly.com/question/12861068
#SPJ1
every year 5 rows and 5columns are increased . derive the formula for the number of students in each row
Answers
The number of students in each row after any number of years, as long as the increase in rows and columns is uniform every year.
Assuming that the increase in rows and columns is uniform every year, we can derive the formula for the number of students in each row as follows:
Let's start with the initial number of rows and columns, which we'll call R0 and C0, respectively, and the number of students in each row, which we'll call S.
After one year, the number of rows and columns will increase by 5, so we'll have R1 = R0 + 5 and C1 = C0 + 5. The total number of students will be R1 x S. We can also express this in terms of the initial number of rows and columns as:
R1 x S = (R0 + 5) x S
Expanding the brackets, we get:
R1 x S = R0 x S + 5 x S
Subtracting R0 x S from both sides, we get:
(R1 - R0) x S = 5 x S
Dividing both sides by 5 x (R1 - R0), we get:
S = 5 / (R1 - R0)
We can use this formula to calculate the number of students in each row after any number of years, as long as the increase in rows and columns is uniform every year.
for such more question on rows and columns
https://brainly.com/question/7331447
#SPJ11
Can someone please help me with this? Explaining would really help thank you
Answers
The solution of the equation is x=1/2 and y=1/3
The given equations are
18x+12y=13...(1)
30x+24y=23...(2)
Let us form the matrix form to solve the equation
[tex]\left[\begin{array}{ccc}18&12\\30&24\end{array}\right] \left[\begin{array}{ccc}x\\y\end{array}\right] =\left[\begin{array}{ccc}13\\23\end{array}\right][/tex]
Multiply equation (1) with 2
36x+24y=26..(3)
Subtract equation 3 from equation 2
30x+24y-36x-24y=23-26
-6x=-3
x=1/2
Now plug in the value of x in equation 1
18(1/2)+12y=13
9+12y=13
12y=4
y=4/12
y=1/3
Hence, the solution of the equation is x=1/2 and y=1/3
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ1
Find the y intercept for a line with a slope or 2 that goes through (5, 4)
Answers
Answer:
y- intercept = - 6
Step-by-step explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
here slope m = 2 , then
y = 2x + c ← is the partial equation
to find c substitute (5, 4 ) into the partial equation
4 = 2(5) + c = 10 + c ( subtract 10 from both sides )
- 6 = c
that is the y- intercept c = - 6
What is the end behavior for f(x) = 2x^3 -3x -4x^4+1
Answers
Based on the given polynomial function, as x approaches positive or negative infinity, the function f(x) = 2x³ - 3x - 4x⁴ + 1 approaches negative infinity.
What is the end behavior of the function?The end behavior of a polynomial function is determined as follows:
Examine the leading term of the function f(x) = -4x⁴ + 2x³ - 3x + 1
The leading term of the function is -4x⁴.
For large positive values of x, as x approaches positive infinity, the leading term -4x⁴ becomes increasingly negative since x⁴ grows faster than any positive constant.
Therefore, the end behavior of the function as x approaches positive infinity is that f(x) approaches negative infinity.
Similarly, for large negative values of x, as x approaches negative infinity, the leading term -4x⁴ becomes increasingly negative since x⁴ grows faster than any positive constant.
Therefore, the end behavior of the function as x approaches negative infinity is that f(x) approaches negative infinity.
Learn more about the end behavior of functions at: https://brainly.com/question/12619590
#SPJ1
100 tickets are sold for $1 each there is $25 prizes and a $10 prize what is the expected value for a person that buys a ticket round to the nearest cent
Answers
The expected value for a person buying a ticket is $0.35 rounded to the nearest cent.
What is the expected value for the person who buys the ticket?The expected value is calculated considering the probabilities of winning each prize and the corresponding values of each prize.
Assuming:
P($25) as the probability of winning the $25 prize
P($10) as the probability of winning the $10 prize
There are 100 tickets sold, therefore, the probabilities can be found as follows:
P($25) = 1/100 (since there is only 1 $25 prize)
P($10) = 1/100 (since there is only 1 $10 prize)
The expected value (E), will then be:
E = P($25) * $25 + P($10) * $10
E = (1/100) * $25 + (1/100) * $10
E = $0.25 + $0.10
E = $0.35
Learn more about expected value at: https://brainly.com/question/14723169
#SPJ1
Using the present value approach, solve the following:
Tom has $100 in a bank account that pays a guaranteed 5% interest rate each year. How much would Tom have at the end of Year 3?
Answers
Answer:
Step-by-step explanation:
$100x0.5x1=$5
please help with geometric series
Answers
Answer:
[tex]C. -5.15\cdot10^{13}[/tex]
Step-by-step explanation:
[tex]Common\ ratio\ (r)=\frac{a_{n+1}}{a_n}=(-3)\\\\Sum\ (S_n)=\frac{a(r^n-1)}{r-1}\ \ (r\neq1)\\\\\implies S_n=\frac{1\ (\ (-3)^{30}-1\ )}{-4}\\\\\implies S_n=\frac{205891132094649-1}{-4}\\\\\approx\frac{206\cdot10^{12}}{-4}\\\\\approx-5.15\cdot10^{13}[/tex]
NO LINKS!!! URGENT HELP PLEASE!!!
3. A virus has infected 400 people in the town and is spreading to 25% more people each day. Write an exponential function to model this situation, then find the number of 3000 people are infected.
4. The population of a small town was 10,800 in 2002. Since then, the population has decreased at a rate of 2.5% each year. Write an exponential function to model the situation, then find when the popuation reaches half the 2002 value?
Answers
Step-by-step explanation:
3. Let P(t) be the number of people infected by the virus at time t (in days). We can model the situation with the following exponential function:
P(t) = 400 * 1.25^t
Here, 400 represents the initial number of infected people, and 1.25 represents the growth factor, since the virus is spreading to 25% more people each day.
To find the number of people infected after t days, we can substitute t = (log(3000) - log(400)) / log(1.25) into the equation:
P(t) = 400 * 1.25^t
P(t) = 400 * 1.25^((log(3000) - log(400)) / log(1.25))
P(t) ≈ 2,343
Therefore, approximately 2,343 people are infected when the total number of infections reaches 3000.
4. Let P(t) be the population of the town at time t (in years). We can model the situation with the following exponential function:
P(t) = 10,800 * 0.975^t
Here, 10,800 represents the initial population in 2002, and 0.975 represents the decay factor, since the population is decreasing at a rate of 2.5% each year.
To find when the population reaches half the 2002 value, we can set P(t) = 5,400 and solve for t:
5,400 = 10,800 * 0.975^t
0.5 = 0.975^t
log(0.5) = t * log(0.975)
t ≈ 28.2
Therefore, the population will reach half the 2002 value in approximately 28.2 years, which corresponds to the year 2030.
Answer:
3) 9.03 days
4) 27.38 years
Step-by-step explanation:
Question 3To model the spread of the virus over time, we can use an exponential function in the form:
[tex]\large\boxed{P(t) = P_0(1 + r)^t}[/tex]
where:
P(t) is the number of infected people after t days.P₀ is the initial number of infected people.r is the daily growth rate (as a decimal).t is the time elapsed (in days).Given the virus has infected 400 people in the town and is spreading to 25% more people each day:
P₀ = 400r = 25% = 0.25Substitute these values into the formula to create a function for P in terms of t:
[tex]P(t) = 400(1 + 0.25)^t[/tex]
[tex]P(t) = 400(1.25)^t[/tex]
To find how many days it will take for 3000 people to be infected, set P(t) equal to 3000 and solve for t:
[tex]\begin{aligned}P(t)&=3000\\\implies 400(1.25)^t&=3000\\(1.25)^t&=7.5 \\\ln (1.25)^t&=\ln(7.5)\\t \ln (1.25)&=\ln(7.5)\\t &=\dfrac{\ln(7.5)}{\ln (1.25)}\\t&=9.02962693...\end{aligned}[/tex]
Therefore, it will take approximately 9.03 days for the virus to infect 3000 people, assuming the daily growth rate remains constant at 25%.
Note: After 9 days, 2980 people would be infected. After 10 days, 3725 people would be infected.
[tex]\hrulefill[/tex]
Question 4To model the population of the town over time, we can use an exponential function in the form:
[tex]\large\boxed{P(t) = P_0(1 - r)^t}[/tex]
where:
P(t) is population after t days.P₀ is the initial population.r is the annual decay rate (as a decimal).t is the time elapsed (in days).Given the initial population was 10,800 and the population has decreased at a rate of 2.5% each year:
P₀ = 10,800r = 2.5% = 0.025Substitute these values into the formula to create a function for P in terms of t:
[tex]P(t) = 10800(1 -0.025)^t[/tex]
[tex]P(t) = 10800(0.975)^t[/tex]
To find how many days it will take for the population to halve, set P(t) equal to 5400 and solve for t:
[tex]\begin{aligned}P(t)&=5400\\\implies 10800(0.975)^t&=5400\\(0.975)^t&=0.5 \\\ln (0.975)^t&=\ln(0.5)\\t \ln (0.975)&=\ln(0.5)\\t &=\dfrac{\ln(0.5)}{\ln (0.975)}\\t&=27.3778512...\end{aligned}[/tex]
Therefore, it will take approximately 27.38 years for the population to reach half the 2002 value, assuming the annual decay rate remains constant at 2.5%.
WHAT IS THE FIRST STEP TO SOLVE 3(4x + 5) = 12
Answers
Multiplying 3 by each term inside the parentheses, we get:
12x + 15 = 12
A cone has a volume of 2560 Pi cm cubed and a height of 30cm. Find the radius
Answers
•A volume of 2560 pi cm cube
•A height of 30 centimeters
The the required one
•The radius of the cone
Then find the solution
Using the formula
V=πr squared * h/3
Solving for
r=3V 3·2560
π·30≈9.02703
πh=
how do u graph the solution y=2x-1 iready
Answers
Answer:
Step-by-step explanation:
y=mx+b
m= slope and b= y intercept
you'll start with a point on the y axis on -1
and the slope will go up so towards the right corner up but 2/1 points