Find the surface area of the prism. Round to the nearest tenth if necessary.
Answers
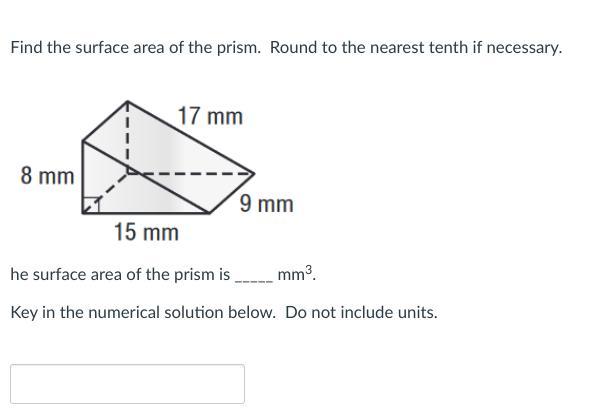
The surface area of the prism is 544 mm²
How to determine the surface area
The formula is given thus;
SA=2B+ph
Where
B = area of the base
p = perimeter of the base
h = height
B = 1/2 h(b1+b2)
B = [tex]\frac{1}{2} * 8 * (17 + 9)[/tex]
B = 108 mm²
Perimeter = sum of length of sides
Perimeter = 17 + 9 + 15
Perimeter = 41 mm
Surface area = 2 ( 108 ) + 41 ( 8)
Surface area = 216 + 328
Surface area = 544 mm²
Thus, the surface area of the prism is 544 mm²
Learn more about surface area of a prism here:
https://brainly.com/question/1297098
#SPJ1
Related Questions
A nurse in a large university (N=30000) is concerned about students eye health. She takes a random sample of 75 students who don’t wear glasses and finds 27 that need glasses.
What the point estimate of p, the population proportion?
Whats the critical z value for a 90% confidence interval for the population proportion?
Whats the margin of error for a 90% confidence interval for the population proportion?
Calculate the 90% confidence interval for the population proportion.
Using your graphing calculator find a 95% confidence interval for the proportion of students who need to wear glasses but done. Show all work.
The nurse wants to be able to estimate, with a 95% confidence interval and a margin of error of 6% the proportion of students who need to wear glasses but don’t. Fine the necessary sample size (n) for this estimate.
Answers
a) p^ = 27/75 = 0.36
what is the one sided p value for zstat 1.72
Answers
The one-sided p value for a z-statistic of 1.72 is approximately 0.0427.
To calculate the one-sided p value for a z-statistic of 1.72:
Step 1: Identify the z-statistic (zstat) given in the question, which is 1.72.
Step 2: Look up the z-statistic in a standard normal (z) table or use an online calculator to find the area to the left of the z-statistic. For a z-statistic of 1.72, the area to the left is approximately 0.9573.
Step 3: Since we want the one-sided p-value, and our z-statistic is positive, we'll calculate the area to the right of the z-statistic. To do this, subtract the area to the left from 1:
P-value (one-sided) = 1 - 0.9573 = 0.0427
The one-sided p-value for a z-statistic of 1.72 is approximately 0.0427.
Learn more about p value here:
https://brainly.com/question/28108646
#SPJ11
unique solution a 1b: 12. let a be an invertible n n matrix, and let b be an n p matrix. explain why a 1b ca
Answers
If a is an invertible n×n matrix and b is an n×p matrix, then the equation ax=b has a unique solution given by [tex]x=a^{-1}b.[/tex]
A⁻¹B is the unique solution to the matrix equation AX = B, given that A is an invertible n x n matrix and B is an n x p matrix.
Based on the given terms, it seems like we want to know why A⁻¹B is a unique solution to the matrix equation AX = B, where A is an invertible n x n matrix and B is an n x p matrix.
A is an invertible n x n matrix, which means it has a unique inverse, A⁻¹.
This is because A is a square matrix and its determinant is non-zero.
B is an n x p matrix.
To find the solution for the matrix equation AX = B, we need to find a matrix X that satisfies this equation.
To solve for X, multiply both sides of the equation by the inverse of A, A⁻¹:
A⁻¹(AX) = A⁻¹B
Since A⁻¹A = I (the identity matrix), the equation becomes:
IX = A⁻¹B
Since the identity matrix times any matrix is the same matrix, X = A⁻¹B.
The uniqueness of the solution comes from the fact that A has a unique inverse, A⁻¹.
If there were multiple inverses, there could be multiple solutions, but since A⁻¹ is unique, so is the solution X.
For similar question on matrix equation.
https://brainly.com/question/28777961
#SPJ11
Find the area of the figure. A composite figure made of a triangle, a square, and a semicircle. The diameter and base measure of the circle and triangle respectively is 6 feet. The triangle has a height of 3 feet. The square has sides measuring 2 feet. area: ft²
Answers
The total area of the figure in this problem is given as follows:
41.3 ft².
How to obtain the area of the composite figure?The area of the composite figure is given by the sum of the areas of all the parts that compose the figure.
The figure in this problem is composed as follows:
Triangle of base 6 feet and height 3 feet.Semicircle of radius 3 feet.Square of side length 2 feet.Then the area of the triangle is given as follows:
At = 0.5 x 6 x 3 = 9 ft².
The area of the semicircle is given as follows:
Ac = π x 3² = 28.3 ft².
The area of the square is given as follows:
As = 2² = 4 ft².
Then the total area of the figure is given as follows:
9 + 28.3 + 4 = 41.3 ft².
More can be learned about area of composite figures at brainly.com/question/10254615
#SPJ1
pls help im kinda desperate
Answers
Answer:
Surface area = 50.27 square feet
Step-by-step explanation:
The formula for surface area (SA) of a sphere is
SA = 4πr^2, where r is the radius.
Although we're not told the radius, we know that C stands for the circumference and the formula for circumference is
C = πd
We know that the radius is half the diameter and since the circumference of the circle is 4π, the radius must be 2 as 4 /2 = 2
Since we now know that the radius of the circle is 2 feet, we can find the volume by plugging it into the formula
SA = 4π * (2)^2
SA = 4π * 4
SA = 16π
SA = 50.26548246
SA = 50.27 square feet
In the tournament described in Exercise 12 of Section 2.4, a top player is defined to be one who either beats every other player or beats someone who beats the other player. Use the WOP to show that in every such tournament with n players there is at least one top player.
Reference: In a certain kind of tournament, every player plays every other player exactly once and either wins or loses. There are no ties. Define a top player to be a player who, for every other player x, either beats x or beats a player y who beats x.
(a) Show that there can be more than one top player.
(b) Use the PMI to show that every n-player tournament has a top player.
Answers
In every n-player tournament described in Exercise 12 of Section 2.4, there is at least one top player.
We will use the Well-Ordering Principle (WOP) to prove that in every n-player tournament, there is at least one top player.
Consider a tournament with n players.
Let's assume that there is no top player in the tournament.
This means that for every player x, there exists a player y who beats x and is beaten by another player z.
We can create a sequence of players: y1, z1, y2, z2, y3, z3, ..., yn, zn, where yi beats xi and is beaten by zi for every i from 1 to n.
Since there are only n players in the tournament, the sequence must repeat at some point due to the Pigeonhole Principle.
Let's say the sequence repeats with players ym and zm, where m < n.
Now, we have a subsequence: ym, zm, ym+1, zm+1, ..., yn, zn, y1, z1, y2, z2, ..., ym-1, zm-1, which is a cycle.
If we consider the players in the cycle from ym to zm-1, none of them can be a top player because they are all beaten by other players within the cycle.
However, we know that ym beats xm and zm-1 beats xm, so by the transitive property, ym must beat zm-1.
This means that ym is a top player, which contradicts our initial assumption.
Therefore, our assumption that there is no top player in the tournament is false.
By the WOP, there must be at least one top player in every n-player tournament.
This proof shows that in every n-player tournament described in Exercise 12 of Section 2.4, there is always at least one top player, as required.
For more questions like Tournament click the link below:
https://brainly.com/question/13219199
#SPJ11
Find the lengths of the sides of the triangle pqr. p(3, 6, 5), q(5, 4, 4), r(5, 10, 1)
Answers
The lengths of the sides of triangle PQR are as follows:
Side PQ: 3 units
Side QR: approximately 6.71 units
Side RP: 6 units
To find the lengths of the sides of triangle PQR, we can utilize the distance formula, which states that the distance between two points (x₁, y₁, z₁) and (x₂, y₂, z₂) in 3D space is given by:
d = √((x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)²)
Now, let's proceed to find the lengths of the sides of triangle PQR.
Side PQ:
The coordinates of points P and Q are P(3, 6, 5) and Q(5, 4, 4) respectively. Applying the distance formula, we have:
PQ = √((5 - 3)² + (4 - 6)² + (4 - 5)²)
= √(2² + (-2)² + (-1)²)
= √(4 + 4 + 1)
= √9
= 3
Therefore, the length of side PQ is 3 units.
Side QR:
The coordinates of points Q and R are Q(5, 4, 4) and R(5, 10, 1) respectively. Using the distance formula, we can calculate the length of side QR:
QR = √((5 - 5)² + (10 - 4)² + (1 - 4)²)
= √(0² + 6² + (-3)²)
= √(0 + 36 + 9)
= √45
≈ 6.71
Hence, the length of side QR is approximately 6.71 units.
Side RP:
To find the length of side RP, we need to calculate the distance between points R(5, 10, 1) and P(3, 6, 5). By applying the distance formula, we get:
RP = √((3 - 5)² + (6 - 10)² + (5 - 1)²)
= √((-2)² + (-4)² + 4²)
= √(4 + 16 + 16)
= √36
= 6
Therefore, the length of side RP is 6 units.
To know more about triangle here
https://brainly.com/question/8587906
#SPJ4
Assume X ~ Poisson(r), where r > 0. Prove that E(X) = r. Show all the steps of the proof.
Answers
This proves that the expected value of a Poisson distribution with parameter r is equal to r.
To prove that E(X) = r for X ~ Poisson(r), we use the definition of expected value:
E(X) = ∑x P(X = x) x
where the sum is taken over all possible values of X, and P(X = x) is the probability that X takes on the value x.
For the Poisson distribution, the probability mass function is:
P(X = x) = (e^-r * r^x) / x!
where r is the parameter of the Poisson distribution, representing the expected number of events per unit time (or space or other interval), and x is a non-negative integer.
Substituting this expression into the definition of expected value, we get:
E(X) = ∑x P(X = x) x
= ∑x (e^-r * r^x) / x! * x
= ∑x (e^-r * r^x) / (x-1)! (using x! = x(x-1)!)
= e^-r ∑x (r^x / (x-1)!)
= e^-r r ∑(x-1) [(r^(x-1)) / ((x-1)!)] (using the substitution k = x-1)
= e^-r r ∑k [(r^k) / k!]
= e^-r r e^r (using the power series expansion of e^r)
Therefore, we have:
E(X) = r
To learn more about probability visit:
brainly.com/question/11234923
#SPJ11
Strong earthquakes occur according to a Poisson process in a metropolitan area with a mean rate of once in 50 years. There are three bridges in the metropolitan area. When a strong earthquake occurs, there is a probability of 0. 3 that a given bridge will collapse. Assume the events of collapse between bridges during a strong earthquake are statistically independent; also, the events of bridge collapse between earthquakes are also statistically independent.
Required:
What is the probability of "no bridge collapse from strong earthquakes" during the next 20 years?
Answers
To find the probability of "no bridge collapse from strong earthquakes" during the next 20 years, we need to calculate the probability of no bridge collapses during the first 20 years, and then multiply it by the probability that no bridge collapses occur during the next 20 years.
The probability of no bridge collapses during the first 20 years is equal to the probability of no bridge collapses during the first 20 years given that no bridge collapses have occurred during the first 20 years, multiplied by the probability that no bridge collapses have occurred during the first 20 years.
The probability of no bridge collapses given that no bridge collapses have occurred during the first 20 years is equal to 1 - the probability of a bridge collapse during the first 20 years, which is 0.7.
The probability that no bridge collapses have occurred during the first 20 years is equal to 1 - the probability of a bridge collapse during the first 20 years, which is 0.7.
Therefore, the probability of "no bridge collapse from strong earthquakes" during the next 20 years is:
1 - 0.7 * 0.7 = 0.27
So the probability of "no bridge collapse from strong earthquakes" during the next 20 years is 0.27
Learn more about probability visit: brainly.com/question/25839839
#SPJ11
Let A = {2,3,4,6,8,9) and define a binary relation among the SUBSETS of A as follows: XRY X and Y are disjoint.. a) Is R symmetric? Explain. b) Is R reflexive? Explain. c) Is R transitive? Explain.
Answers
a) No, R is not symmetric. b) No, R is not reflexive. c) Yes, R is transitive.
To see this, consider the subsets {2, 4} and {3, 6}. These subsets are disjoint, so {2, 4}R{3, 6}. However, {3, 6} is also disjoint from {2, 4}, so {3, 6}R{2, 4} is not true. For any subset X of A, X and the empty set are disjoint, so XRX cannot be true. To see this, suppose that XRY and YRZ, where X, Y, and Z are subsets of A. Then X and Y are disjoint, and Y and Z are disjoint. Since the empty set is disjoint from any set, we have that X and Z are disjoint as well. Therefore, X and Z satisfy the definition of the relation, so XRZ is true. A binary relation R across a set X is reflexive if each element of set X is related or linked to itself.
Learn more about reflexive here:
https://brainly.com/question/29119461
#SPJ11
Choose a random integer X from the interval [0,4]. Then choose a random integer Y from the interval [0,x], where x is the observed value of X. Make assumptions about the marginal pmf fx(x) and the conditional pmf h(y|x) and compute P(X+Y>4).
Answers
Making assumptions about the marginal pmf fx(x) and the conditional pmf h(y|x), probability P(X+Y>4) is 0.35.
To compute P(X+Y>4), we need to consider the possible values of X and Y and calculate the probabilities accordingly.
Let's analyze the scenario step by step:
Randomly choosing X from the interval [0, 4]:
The possible values for X are 0, 1, 2, 3, and 4. We assume a uniform distribution for X, meaning each value has an equal probability of being chosen. Therefore, the marginal pmf fx(x) is given by:
fx(0) = 1/5
fx(1) = 1/5
fx(2) = 1/5
fx(3) = 1/5
fx(4) = 1/5
Choosing Y from the interval [0, x]:
Since the value of X is observed, the range for Y will depend on the chosen value of X. For each value of X, Y can take on values from 0 up to X. We assume a uniform distribution for Y given X, meaning each value of Y in the allowed range has an equal probability. Therefore, the conditional pmf h(y|x) is given by:
For X = 0: h(y|0) = 1/1 = 1
For X = 1: h(y|1) = 1/2
For X = 2: h(y|2) = 1/3
For X = 3: h(y|3) = 1/4
For X = 4: h(y|4) = 1/5
Computing P(X+Y>4):
We want to find the probability that the sum of X and Y is greater than 4. Since X and Y are independent, we can calculate the probability using the law of total probability:
P(X+Y>4) = Σ P(X+Y>4 | X=x) * P(X=x)
= Σ P(Y>4-X | X=x) * P(X=x)
Let's calculate the probabilities for each value of X:
For X = 0: P(Y>4-0 | X=0) * P(X=0) = 0 * 1/5 = 0
For X = 1: P(Y>4-1 | X=1) * P(X=1) = 1/2 * 1/5 = 1/10
For X = 2: P(Y>4-2 | X=2) * P(X=2) = 1/3 * 1/5 = 1/15
For X = 3: P(Y>4-3 | X=3) * P(X=3) = 1/4 * 1/5 = 1/20
For X = 4: P(Y>4-4 | X=4) * P(X=4) = 1/5 * 1/5 = 1/25
Summing up the probabilities:
P(X+Y>4) = 0 + 1/10 + 1/15 + 1/20 + 1/25
= 0.35
Therefore, the probability P(X+Y>4) is 0.35.
To learn more about probability here:
https://brainly.com/question/32117953
#SPJ4
I spent 3/4 of this weeks allowance on candy. Of the money she spent on candy, 56 was spent on gummy bears. What fraction of this weeks allowance does ice spend on gummy bears
Answers
The fraction of this week's allowance spent on gummy bears is 56/x. The money spent on candy will be 3/4x. Now, out of the total amount spent on candy, 56 were spent on gummy bears.
Given that,
56 was spent on gummy bears.
I spent 3/4 of this week's allowance on candy.
Let the week's allowance be x
Therefore, money spent on candy = 3/4 of x = (3/4)x
To find:
A fraction of this week's allowance is spent on gummy bears.
Now, we know that 56 was spent on gummy bears.
Therefore, the fraction of this week's allowance spent on gummy bears is 56/x.
To know more about the fraction, visit :
brainly.com/question/10354322
#SPJ11
Suppose that you have obtained data by taking a random sample from a population and that you intend to find a confidence interval for the population mean, μ which confidence level, 95% or 99%, will result in the confidence interval giving a more accurate estimate of μ? Choose the correct answer below. A. Both will have the same accuracy or the estimate o μ since only variations in sample szes affect the accuracy for the estimate of confidence levels are being applied to the same sample. B. The 95% confidence level will give a more accurate estimate of μ since the margin of error will be smaller for this confidence level
C. The 99% confidence level will give a more accurate estimate of μ since the confidence level is higher. D. The 99% confidence level will give a more accurate estimate of μ since the margin of error will be smaller for this confidence level.
Answers
The confidence interval for the population mean, μ which confidence level, 95% or 99%, will result in the confidence interval giving a more accurate estimate of μ is :
D. The 99% confidence level will give a more accurate estimate of μ since the margin of error will be smaller for this confidence level.
When constructing a confidence interval for the population mean, increasing the confidence level will result in a wider interval, as there is a higher level of certainty that the true population mean falls within the interval. However, a wider interval means that the margin of error, or the amount by which the interval is likely to differ from the true population mean, will also be larger.
Therefore, if we want a more precise estimate of the population mean, we should choose a confidence level that results in a smaller margin of error. Since the margin of error decreases as the confidence level decreases, the 99% confidence level will give a more accurate estimate of μ than the 95% confidence level.
Therefore, the correct answer is : (D)
To learn more about the confidence level visit : https://brainly.com/question/17097944
#SPJ11
Given: f(x) = 5x/x2 +6x+8 A.Find the horizontal asymptote(s) for the function. (Use limit for full credit.) B. (8 pts) Find the vertical asymptote(s) for the function.
Answers
The function f(x) = 5x/(x^2 + 6x + 8) has vertical asymptotes at x = -2 and x = -4.
What are the horizontal and vertical asymptotes for the given function f(x) = 5x/(x^2 + 6x + 8)?A. To find the horizontal asymptote(s) for the function, we need to take the limit as x approaches infinity and negative infinity.
lim x→∞ f(x) = lim x→∞ 5x/(x² + 6x + 8)= lim x→∞ 5/x(1 + 6/x + 8/x²)= 0lim x→-∞ f(x) = lim x→-∞ 5x/(x² + 6x + 8)= lim x→-∞ 5/x(1 + 6/x + 8/x²)= 0
Therefore, the horizontal asymptote is y = 0.
B. To find the vertical asymptote(s) for the function, we need to determine the values of x that make the denominator of the function equal to zero.
x² + 6x + 8 = 0
We can factor this quadratic equation as:
(x + 2)(x + 4) = 0
Therefore, the vertical asymptotes are x = -2 and x = -4.
Learn more about quadratic equation
brainly.com/question/1863222
#SPJ11
determine whether the series converges or diverges. [infinity] 5^n 1 4n − 2 n = 1
Answers
To determine whether the series converges or diverges, we need to analyze the given series. The series is:
Σ (5^n / (4n - 2)), from n = 1 to infinity.
To check for convergence, we can apply the Ratio Test, which involves finding the limit of the ratio between consecutive terms. Let's denote the term a_n as (5^n / (4n - 2)). Then, we'll compute the limit as n approaches infinity:
lim (n→∞) (a_(n+1) / a_n) = lim (n→∞) ((5^(n+1) / (4(n+1) - 2)) / (5^n / (4n - 2)))
Simplifying this expression, we get:
lim (n→∞) (5^(n+1) / 5^n) * ((4n - 2) / (4(n+1) - 2))
The first part of the limit simplifies to:
lim (n→∞) 5 = 5
The second part of the limit becomes:
lim (n→∞) ((4n - 2) / (4n + 2)) = 1
Multiplying both limits, we get:
5 * 1 = 5
Since the limit is greater than 1, the Ratio Test indicates that the series diverges.
Learn more about Ratio Test: https://brainly.com/question/29579790
#SPJ11
Solve this taylor series f'(x)=3f(x) 10 and f(0)=2
Answers
The Taylor series of the function f(x) = f(0) + f'(0)x + (f''(0)x^2)/2! + (f'''(0)x^3)/3! + ... for f'(x) = 3f(x) and f(0) = 2 is:
f(x) = 2 + 6x + 9x^2 + (9/2)x^3 + (27/8)x^4 + ...
To find the Taylor series of f(x), we need to first find the derivatives of f(x) and evaluate them at x=0. Given that f'(x) = 3f(x) and f(0) = 2, we can start by finding the first few derivatives of f(x) and evaluating them at x=0:
f'(x) = 3f(x)
f''(x) = 3f'(x) = 9f(x)
f'''(x) = 9f'(x) = 27f(x)
f''''(x) = 27f'(x) = 81f(x)
Evaluating these derivatives at x=0, we get:
f(0) = 2
f'(0) = 3f(0) = 6
f''(0) = 9f(0) = 18
f'''(0) = 27f(0) = 54
f''''(0) = 81f(0) = 162
Now we can use these values to write out the Taylor series of f(x):
f(x) = f(0) + f'(0)x + (f''(0)x^2)/2! + (f'''(0)x^3)/3! + (f''''(0)x^4)/4! + ...
= 2 + 6x + (18x^2)/2! + (54x^3)/3! + (162x^4)/4! + ...
= 2 + 6x + 9x^2 + (9/2)x^3 + (27/8)x^4 + ...
Therefore, the Taylor series of f(x) is given by:
f(x) = 2 + 6x + 9x^2 + (9/2)x^3 + (27/8)x^4 + ...
Learn more about Taylor series :
https://brainly.com/question/29733106
#SPJ11
Each day, Farzana makes fresh egg salad for her sandwich shop. She makes 5 pounds of egg salad each day, Monday through Saturday. On Sunday, she makes 8. 3 pounds of egg salad. How much egg salad does Farzana make each week?
Answers
Farzana makes 38.3 pounds of egg salad each week for her sandwich shop.
Farzana makes 5 pounds of egg salad each day from Monday to Saturday, totaling 6 days. On Sunday, she makes 8.3 pounds of egg salad. To calculate the total amount of egg salad Farzana makes in a week, we need to add up the amounts from each day.
From Monday to Saturday, she makes a total of 5 pounds * 6 days = 30 pounds of egg salad.
On Sunday, she makes 8.3 pounds of egg salad.
To find the total amount for the week, we add the amounts from Monday to Saturday to the amount from Sunday:
30 pounds + 8.3 pounds = 38.3 pounds
Therefore, Farzana makes 38.3 pounds of egg salad each week for her sandwich shop.
To learn more about pounds here:
https://brainly.com/question/29291054
#SPJ4
A group bought 12 movie tickets that cost a total of $120. How many student tickets were bought? Student tickets cost $9 each
Adult tickets cost $12 each
Answers
Let x be the number of student tickets and y be the number of adult tickets. There are 12 tickets total. Therefore: `x + y = 12`The cost of student tickets is $9 and the cost of adult tickets is $12.
We know that the cost of all 12 tickets is $120. Therefore: `9x + 12y = 120`We can solve this system of equations by substitution or elimination.
Let's use substitution: Solve the first equation for `x`: `x = 12 - y`Substitute that into the second equation: `9(12 - y) + 12y = 120`Simplify and solve for `y`: `108 - 9y + 12y = 120` `3y = 12` `y = 4`Now we know that 4 adult tickets were bought. We can substitute that back into the first equation to find the number of student tickets: `x + 4 = 12` `x = 8`Therefore, 8 student tickets were bought.
Know more about system of equations here:
https://brainly.com/question/20067450
#SPJ11
0.85m plus 7.5 = 12.6
find the value of m :)
Answers
Answer: m = 6
Step-by-step explanation: In a calculator, I put in the following equation:
12.6 = 0.85m + 7.5
and that have me the answer of 6
We can double check this solution by putting the following equation in the calculator:
(0.85 x 6) + 7.5 =
and you will see that is = to 12.6
Answer:
m = 6
Step-by-step explanation:
Isolate the variable, m. Note the equal sign, what you do to one side, you do to the other. Do the opposite of PEMDAS.
PEMDAS is the order of operations, and stands for:
Parenthesis
Exponents (& Roots)
Multiplications
Divisions
Additions
Subtractions
~
First, subtract 7.5 from both sides of the equation:
[tex]0.85m + 7.5 = 12.6\\0.85m + 7.5 (-7.5) = 12.6 (-7.5)\\0.85m = 12.6 - 7.5\\0.85m = 5.1[/tex]
Next, isolate the variable, m, by dividing 0.85 from both sides of the equation:
[tex]0.85m = 5.1\\\frac{(0.85m)}{0.85} = \frac{(5.1)}{0.85} \\m = \frac{5.1}{0.85} \\m = 6[/tex]
6 would be your value for m.
~
Learn more about solving with PEMDAS, here:
https://brainly.com/question/29172059
find an equation for the plane passing through the points (0, 2, 1), (1, 1, 5), and (2, 0, 11).
Answers
The equation of the plane passing through the points (0, 2, 1), (1, 1, 5), and (2, 0, 11) is 12x - 6y - 10z = 0.
To find the equation of the plane passing through three given points, the point-normal form of the equation. This form uses a point on the plane and the normal vector perpendicular to the plane.
Step 1: Find two vectors on the plane by subtracting the coordinates of one point from the other two points.
Vector 1 = (1, 1, 5) - (0, 2, 1) = (1, -1, 4)
Vector 2 = (2, 0, 11) - (0, 2, 1) = (2, -2, 10)
Step 2: Calculate the cross product of the two vectors to obtain the normal vector to the plane.
Normal vector = Vector 1 × Vector 2
Using the determinant method:
i j k
1 -1 4
2 -2 10
= (1 × 10 - (-1) × (-2))i - (1 × 10 - 4 × (-2))j + (-1 × (-2) - 4 × 2)k
= 12i - 6j - 10k
Therefore, the normal vector is (12, -6, -10).
Step 3: Choose one of the given points as the reference point on the plane. Let's choose (0, 2, 1) as the reference point.
Step 4: Substitute the values into the point-normal form of the equation:
(x - x₁)(A) + (y - y₁)(B) + (z - z₁)(C) = 0
Where (x₁, y₁, z₁) is the reference point, and (A, B, C) are the components of the normal vector.
Substituting the values,
(x - 0)(12) + (y - 2)(-6) + (z - 1)(-10) = 0
Simplifying the equation:
12x - 6y - 10z + 12 - 12 = 0
12x - 6y - 10z = 0.
To know more about equation here
https://brainly.com/question/30336283
#SPJ4
the probability that a marriage will end in divorce within 10 years is . what are the mean and standard deviation for the binomial distribution involving marriages?
Answers
The mean (expected value) of a binomial distribution is equal to the product of the number of trials and the probability of success on each trial. Therefore, the mean of the binomial distribution for marriages would be 10 multiplied by the probability of divorce within 10 years. The standard deviation of a binomial distribution is equal to the square root of the product of the number of trials, the probability of success on each trial, and the probability of failure on each trial. Since the probability of success (divorce) is already known, we can calculate the probability of failure (not divorcing) by subtracting the probability of success from 1.
The binomial distribution is a discrete probability distribution that describes the number of successes in a fixed number of independent trials. In the case of marriages, the number of trials is 10 years, and the success is divorce within that time period. The probability of divorce within 10 years is not provided in the question, but let's assume it is 50% for the sake of simplicity. Therefore, the mean of the binomial distribution would be 10 multiplied by 0.5, which equals 5. The standard deviation would be the square root of (10 x 0.5 x 0.5), which equals 1.58.
In summary, the mean and standard deviation for the binomial distribution involving marriages depend on the probability of divorce within the specified time period. The mean is equal to the number of years multiplied by the probability of divorce, while the standard deviation is equal to the square root of the product of the number of years, the probability of divorce, and the probability of not divorcing. These calculations can be used to understand the expected number of divorces and the variability around that expectation.
To know more about bionomial distribution visit:
https://brainly.com/question/9295333
#SPJ11
As the Gibbs sampler progresses; the samples can be assumed to be coming from the O prior conditional distributions given the (b) O posterior The inclusion of the sampling of the (b;) means the Gibbs sampler does not converge.
Answers
Including the sampling of the (b) parameter in the Gibbs sampler can lead to issues with convergence.
In the Gibbs sampler, as it progresses, the samples are assumed to be drawn from the prior conditional distributions given the observed data. However, if the sampling of a particular variable is included, such as the (b) parameter, the Gibbs sampler may not converge.
The Gibbs sampler is a Markov chain Monte Carlo (MCMC) algorithm used for drawing samples from a joint distribution when the conditional distributions are easier to sample from individually. In each iteration of the Gibbs sampler, the values of variables are updated one at a time based on their conditional distributions.
Ideally, the Gibbs sampler aims to converge to the target distribution, allowing for efficient estimation and inference. However, the inclusion of certain variables in the sampling process can affect the convergence properties of the sampler. Specifically, if the (b) parameter is sampled in the Gibbs sampler, it may prevent convergence.
The convergence of the Gibbs sampler relies on the Markov chain satisfying certain conditions, such as irreducibility, aperiodicity, and ergodicity. When a parameter like (b) is included, it may introduce dependencies or correlations that violate these conditions, preventing the sampler from reaching a stationary distribution.
Therefore, including the sampling of the (b) parameter in the Gibbs sampler can lead to issues with convergence. It is important to carefully consider the impact of including or excluding variables in the sampling process and assess the convergence properties of the Gibbs sampler in each specific case.
Learn more about convergence here:
https://brainly.com/question/28202684
#SPJ11
the base of the triangle is 4 more than the width. the area of the rectangle is 15. what are the dimensions of the rectangle?
Answers
If the area of the rectangle is 15, the dimensions of the rectangle are l = √(15) and w = √(15).
The question is referring to a rectangle, we can use the formula for the area of a rectangle, which is A = lw, where A is the area, l is the length, and w is the width.
We are given that the area of the rectangle is 15, so we can set up an equation:
l * w = 15
We are not given any information about the length, so we cannot solve for l and w separately. However, if we assume that the rectangle is a square (i.e., l = w), then we can solve for the dimensions:
l * l = 15
l² = 15
l = √(15)
To learn more about rectangle click on,
https://brainly.com/question/13129748
#SPJ1
. determine all horizontal asymptotes of f(x) = [x-2]/[x^2 1] 2 determine all vertical asymptotes of f(x) = [x-2]/[x^2-11] 2
Answers
A horizontal asymptote is a straight line that a function approaches as x approaches infinity or negative infinity.
For the function f(x) = (x-2)/(x^2 + 1):
Horizontal asymptotes:
As x approaches infinity or negative infinity, the highest degree term in the numerator and denominator are the same, which is x^2. Therefore, we can use the ratio of the coefficients of the highest degree terms to determine the horizontal asymptote. In this case, the coefficient of x^2 in both the numerator and denominator is 1. So the horizontal asymptote is y = 0.
Vertical asymptotes:
Vertical asymptotes occur when the denominator of a rational function equals zero and the numerator does not. So, to find the vertical asymptotes of f(x), we need to solve the equation x^2 + 1 = 0. However, this equation has no real solutions, which means that there are no vertical asymptotes for f(x).
For the function f(x) = (x-2)/(x^2 - 11):
Vertical asymptotes:
To find the vertical asymptotes, we need to solve the equation x^2 - 11 = 0. This equation has two real solutions, which are x = sqrt(11) and x = -sqrt(11). These are the vertical asymptotes of f(x).
Horizontal asymptotes:
As x approaches infinity or negative infinity, the highest degree term in the numerator and denominator are x and x^2 respectively. Therefore, the horizontal asymptote is y = 0. However, we also need to check if there are any oblique asymptotes. To do this, we can use long division or synthetic division to divide the numerator by the denominator. After doing this, we get:
x - 2
--------------
x^2 - 11 | x - 2
x - sqrt(11)
------------
sqrt(11) + 11
sqrt(11) + 2
--------------
-9
Since the remainder is a non-zero constant (-9), there are no oblique asymptotes. So the only asymptotes for f(x) are the vertical asymptotes x = sqrt(11) and x = -sqrt(11).
To learn more about asymptote visit:
brainly.com/question/28822186
#SPJ11
given the parabola below, find the endpoints of the latus rectum. (x−2)2=−8(y−7)
Answers
The endpoints of the latus rectum of the parabola with equation [tex](x-2)^{2}[/tex] = -8(y-7) are (2, 7) and (2, -9).
The given equation of the parabola is in the form [tex](x-h)^{2}[/tex] = 4p(y-k), where (h, k) represents the vertex and 4p represents the length of the latus rectum. Comparing this with the given equation [tex](x-2)^{2}[/tex] = -8(y-7), we can see that the vertex is (2, 7) since (h, k) = (2, 7). The coefficient of (y-7) is -8, so 4p = -8, which implies p = -2. Since the latus rectum is a line passing through the focus and perpendicular to the axis of symmetry, its length is equal to 4p. Thus, the length of the latus rectum is 4(-2) = -8. The latus rectum is parallel to the x-axis, and its endpoints can be found by adding and subtracting the length of the latus rectum to the y-coordinate of the vertex. Hence, the endpoints of the latus rectum are (2, 7 + (-8)) = (2, -1) and (2, 7 - (-8)) = (2, 15), or in simplified form, (2, -9) and (2, 7).
learn more about parabola here:
https://brainly.com/question/29267743
#SPJ11
the table defines a discrete probability distribution. find the expected value of the distribution. x 0 1 2 3 pr(x) 3/16 3/16 1/8 1/2
Answers
To find the expected value of a discrete probability distribution, we multiply each possible outcome by its probability and then sum the products. In this case, we have:
E(X) = 0(3/16) + 1(3/16) + 2(1/8) + 3(1/2)
= 0 + 3/16 + 1/4 + 3/2
= 1.5
Therefore, the expected value of this distribution is 1.5.
In probability theory, the expected value (also known as the mean or average) of a discrete probability distribution is a measure of the central tendency of the distribution. It represents the theoretical long-term average of the values taken by a random variable over an infinite number of trials.
To find the expected value of a discrete probability distribution, we multiply each possible value of the random variable by its corresponding probability and add up the products. In other words, if X is a discrete random variable with possible values x1, x2, ..., xn and corresponding probabilities p1, p2, ..., pn, then the expected value E(X) is:
E(X) = x1 * p1 + x2 * p2 + ... + xn * pn
For example, consider the discrete probability distribution given in the table:
x | 0 | 1 | 2 | 3
pr(x) | 3/16| 3/16| 1/8 | 1/2
To find the expected value of this distribution, we multiply each possible value of X by its corresponding probability and add up the products:
E(X) = 0*(3/16) + 1*(3/16) + 2*(1/8) + 3*(1/2) = 0 + 0.1875 + 0.25 + 1.5 = 1.9375
Therefore, the expected value of this distribution is 1.9375.
To learn more about discrete probability distribution refer below
https://brainly.com/question/9602705
#SPJ11
explain what the P-value means in this context. choose the correct answer below.a. the probability of observing a sample mean lower than 43.80 is 1.1% assuming the data come from a population that follows a normal model.b. the probability of observing a sample mean lower than 40.8 is 1.1% assuming the data come from a population that follows a normal model.c. if the average fuel economy is 43.80 mpg,the chance of obtaining a population mean of 40.8 or more by natural sampling variation is 1.1%d. if the average fuel economy is 40.8 mpg,the chance of obtaining a population mean of 43.80 or more by natural sampling variation is 1.1%
Answers
The probability of observing a sample mean lower than 40.8 is 1.1% assuming the data come from a population that follows a normal model. Therefore, option b. is correct.
The p-value is a measure of the evidence against a null hypothesis. In statistical hypothesis testing, the null hypothesis is typically a statement of "no effect" or "no difference" between two groups or variables. The p-value represents the probability of obtaining a sample statistic (or one more extreme) if the null hypothesis is true.
In this context, the p-value is 1.1%, which means that if the null hypothesis were true (i.e., the population mean is equal to 43.80), the probability of obtaining a sample mean lower than 40.8 is 1.1%. This suggests that the data provide some evidence against the null hypothesis and support the alternative hypothesis that the population mean is less than 43.80.
for such more question on probability
https://brainly.com/question/13604758
#SPJ11
The correct answer is a. The P-value represents the probability of observing a sample mean as extreme or more extreme than the one observed, assuming that the data comes from a population that follows a normal model.
In this context, a P-value of 1.1% means that there is a low probability of observing a sample mean lower than 43.80, given that the data comes from a normal distribution. This suggests that the observed sample mean is unlikely to have occurred by chance alone, and provides evidence for a significant difference between the sample mean and the hypothesized population mean.
The P-value represents the probability of observing a sample mean as extreme as, or more extreme than, the one obtained from your data (43.80 mpg) if the true population mean is 40.8 mpg. The P-value of 1.1% indicates that there is a 1.1% chance of obtaining a sample mean of 43.80 or more due to natural sampling variation, assuming the population follows a normal model.
To learn more about probability : brainly.com/question/31828911
#SPJ11
Use the Integral Test to determine whether the series is convergent or divergent 14 n=1 Step 1 In order to apply the Integral Test for the function f(x) on the interval [a, co), which of the following must be true? (Select all that apply.) P | f is continuous f is differentiable. f is positive. f is negative. f is increasing.f is decreasing. Step 2 For Σ 11 , since rx)=11 , since f(X) =- is continuous, positive, and decreasing on [1,。。), we consider the following. 14 n=1 (If the quantity diverges, enter DIVERGES.)
Answers
The integral diverges, the series Σ11/n also diverges by the Integral Test. Therefore, the answer is DIVERGES.
To apply the Integral Test, the function f(x) must be continuous, positive, and decreasing on the interval [a, ∞).
In this case, we are considering the series Σ11/n. We can define the function f(x) = 1/x, which is continuous, positive, and decreasing on the interval [1, ∞).
Now, we can apply the Integral Test:
∫1∞ 1/x dx = lim t→∞ ln(t) - ln(1) = ∞
Since the integral diverges, the series Σ11/n also diverges by the Integral Test. Therefore, the answer is DIVERGES.
for such more question on integral diverges
https://brainly.com/question/22008756
#SPJ11
Assume that all grade point averages are to be standardized on a scale between 0 and 4. How many grade point averages must be obtained so that the sample mean is within. 01 of the population mean? assume that a 99% confidence level is desired. If using range rule of thumb
Answers
We would need a sample size of approximately 167 grade point averages to ensure that the sample mean is within 0.01 of the population mean with a 99% confidence level using the range rule of thumb.
To ensure that the sample mean is within 0.01 of the population mean with a 99% confidence level, the number of grade point averages needed depends on the standard deviation of the population. The answer can be obtained using the range rule of thumb.
The range rule of thumb states that for a normal distribution, the range is typically about four times the standard deviation. Since we want the sample mean to be within 0.01 of the population mean, we can consider this as the range.
A 99% confidence level corresponds to a z-score of approximately 2.58. To estimate the standard deviation of the population, we need to assume a sample size. Let's assume a conservative estimate of 30, which is generally considered sufficient for the Central Limit Theorem to apply.
Using the range rule of thumb, the range would be approximately 4 times the standard deviation. So, 0.01 is equivalent to 4 times the standard deviation.
To find the standard deviation, we divide 0.01 by 4. So, the estimated standard deviation is 0.0025.
To determine the number of grade point averages needed, we can use the formula for the margin of error in a confidence interval: Margin of Error = (z-score) * (standard deviation / √n).
Rearranging the formula to solve for n, we have n = ((z-score) * standard deviation / Margin of Error)².
Plugging in the values, n = ((2.58) * (0.0025) / 0.01)² = 166.41.
Learn more about sample mean:
https://brainly.com/question/31101410
#SPJ11
Find location of local maxima or local minima over the interval [0,2π]. g(x)=cosx/2+sinx
Answers
The function g(x) = (cos(x))/2 + sin(x) has a local minimum at x = π/6 and a local maximum at x = 7π/6 over the interval [0,2π].
1) Find the critical points of g(x) over the interval [0,2π]:
g'(x) = (-sin(x))/2 + cos(x)
Setting g'(x) = 0, we get:
(-sin(x))/2 + cos(x) = 0
cos(x) = (1/2)sin(x)
Using the identity sin^2(x) + cos^2(x) = 1, we can rewrite this as:
sin(x) = ±√3/2 cos(x)
Solving for x, we get:
x = π/6, 5π/6, 7π/6, 11π/6
2) Classify the critical points as local maxima, local minima or saddle points by using the first or second derivative test:
g''(x) = (-cos(x))/2 - sin(x)
At x = π/6, g'(π/6) = 1/2 and g''(π/6) = -√3/2 < 0, which means that x = π/6 is a local minimum.
At x = 5π/6, g'(5π/6) = -1/2 and g''(5π/6) = -√3/2 < 0, which means that x = 5π/6 is a local minimum.
At x = 7π/6, g'(7π/6) = -1/2 and g''(7π/6) = √3/2 > 0, which means that x = 7π/6 is a local maximum.
At x = 11π/6, g'(11π/6) = 1/2 and g''(11π/6) = √3/2 > 0, which means that x = 11π/6 is a local maximum.
3) Check the endpoints of the interval [0,2π] to see if they are local maxima or minima:
g(0) = 0.5, g(2π) = -0.5
Neither g(0) nor g(2π) are critical points, so they cannot be local maxima or minima.
Therefore, the function g(x) = (cos(x))/2 + sin(x) has a local minimum at x = π/6 and a local maximum at x = 7π/6 over the interval [0,2π].
Learn more about local maxima or minima:
https://brainly.com/question/29167373
#SPJ11